20230118 Bird call identification

Problem

It would be good to stick a recorder in a forest to monitor bird calls. That way you could get population density estimates and so on and so forth. There are some existing approaches that do this already but they all require labelled data, which is pretty sparse and of course limits you to stuff you have already seen. The question is whether or not you can train a system to be able to identify bird calls without human labelled data. I think this might be possible.

Idea: Multiple Microphone Math

The overarching idea here is that by placing many microphones in a section of forest bird calls will be audible from multiple microphones and hence locatable in space and amplitude since the position of the microphones are known (think gps satellites in known locations solving for receivers in unknown locations). This means that for a given call the microphones will receive bird call recordings that are a bit different in time, volume, and background noise. However as the organiser of this system we know that the bird call recordings belong to the same bird making the same call. So whilst we don’t know necessarily what the bird is in these recordings, we do know that it is the same one.

Note that if there are fewer bird calls then there are microphones it’s possible to solve uniquely for the location of the bird and extract the bird call itself from the other bird calls and background noise. This would help a great deal I think in creating clean recordings for training. Once you have a large set of these clean recordings you can then easily simulate many bird calls at once by mixing your pristine recordings together to create a big synthetic bird chorous, and then train your net on this. Then you can go back to the real mucky bird chorouses and run the identification for real. You’ll need buckets of data for this I suspect, but that’s exactly what a system like this is supposed to provide.

Problem: splitting recordings

What gets recorded will of course be N streams of audio from the N microphones. This needs to be split into discrete chunks around bird calls. Undoubtedly this will require piles and piles of disgusting heuristics but once again our multiple receivers will help here. A proposal: find a loud identifiable bit of the recording via a simple threshold or something. With all the microphones you can then locate this recording in space and create a synthetic microphone that listens only to that point in space. This is very cool but also understandably makes it much easier to tell when the call started and stopped since it solves the problem of the end of one call overlapping with the start of another that you don’t really have any way to solve with a single microphone.

20230703 note

Maybe what we want here is “contrastive” learning?

Problem: $cro{w}_t==cro{w}_{t+1}$ ??

The above notes show how to locate, separate and label a call that happens at a certain time by a certain bird. But it does not give insight as to how a bird that calls on two separate occasions gets labelled the same thing both times. I do not know how to solve this. I think that with a sufficient number of examples it’s pretty likely that different occurrences of the same call will end up in similar places in the embedding space, so maybe a traditional clustering algorithm could be used? This is I think the biggest flaw with this method, though. I’m sure that there are many many examples of how to do this in the literature though since this problem is the same problem as identifying different pronounciations of the same word in a speech dataset, and there’s loads of research one speech recognition.

More maths

Simplest case first

Let me try and get down some problem statements first. Consider the simplest scenario: there is a single bird that sends a single pulse of sound to a bunch of microphones.

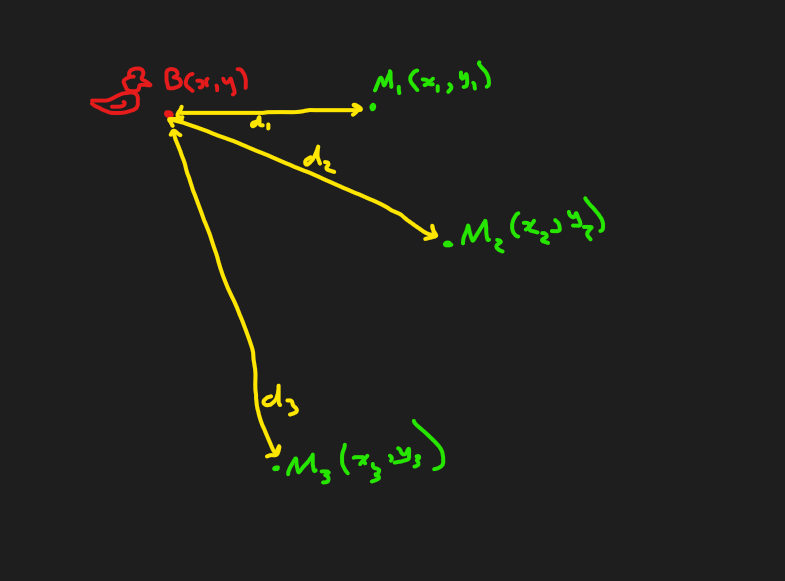Remembering that distance is the same as time here what we observe in this case is that microphone $M_1$ hears something, then $M_2$, then $M_3$. So the input to our system/our observation is $[0,d_1-d_2,d_1-d_3]$. Call the microphone array $M=[M_1...M_3]$. Since we know the positions in M I do believe we are one linear equation away for writing down the location of the bird $B$ which one can solve in a least squares fashion in numpy. If you write down the matrices in the right way you can just keep adding more $M$ and $B$ provided that $M$ is sufficiently bigger than $B$. I’m sure you could put down like 10 microphones in practice, so that’s enough to get quite a few birdcalls.

How many birds?

The above is how to calculate where the birds are given how many of them exist, but not how many of them there are. I think you could do this iteratively by looking at how well the solution fits when you assume one bird, then two, then three etc. This will be greatly confused by bird calls with quite different volumes, and also by background noise.

More assumptions

• When a bird is far away it might be audible to only a subset of the microphones.
• Do birds call whilst moving?
• The positional accuracy here prolly won’t be that great what with all the trees and stuff. So birds that are close together will cause problems.
• Perhaps real recordings just have so many sources all the time that it’s hard to get enough single-call data to train on.