20230604 Simulate trivialities

n body is not so trivial

Before I said that an n body simulation would be trivial. But it turns out that it might be quite so much as I had thought. I wrote a simple n body simulation:

That whilst not particularly accurate because of floating point shenanigans, nonetheless behaves in a predictable way.

State

The state of each particle is a 5 dimensional vector - [mass, x, y, vx, vy]. So a 10-particle system is a 10x5 matrix.

Initial attempt

I initially copy/pasted hacked together a trivial Graph convolutional neural net using the pytorch geometric framework:

GCN

 
 
class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super().__init__(aggr='add')  # "Add" aggregation (Step 5).
        self.project_in = Linear(in_channels, out_channels, bias=False)
 
        # self.edge_lin = Linear(2 * out_channels, out_channels)
        self.message_join = Linear(2 * out_channels, out_channels, bias=False)
        self.edge_mlp = Seq(Linear(2 * out_channels, out_channels),
                       ReLU(),
                       Linear(out_channels, out_channels))
 
        self.reset_parameters()
 
    def reset_parameters(self):
        self.project_in.reset_parameters()
        self.message_join.reset_parameters()
 
    def forward(self, x, edge_index):
        x = self.project_in(x)
        # Step 4-5: Start propagating messages.
        messages = self.propagate(edge_index, x=x)
        out = self.message_join(torch.cat((x, messages), dim=1))
 
        return out
 
    def message(self, x_i, x_j):
        tmp = torch.cat([x_i, x_j - x_i], dim=1)  # tmp has shape [E, 2 * in_channels]
        return self.edge_mlp(tmp)
 
 
class GCN(torch.nn.Module):
    def __init__(self, num_features: int):
        super().__init__()
        hidden_size = nbody.NUM_STATES
        self.input_conv = GCNConv(num_features, hidden_size)
        self.hidden_conv1 = GCNConv(hidden_size, hidden_size)
        self.hidden_conv2 = GCNConv(hidden_size, hidden_size)
        # self.output_conv = GCNConv(hidden_size, num_features)
 
    def forward(self, x):
        # ChatGpt special to generate edge index for fully connected graph:
        edge_index = torch.combinations(torch.arange(x.shape[0]), with_replacement=False).t().contiguous()
        edge_index = torch.cat((edge_index, edge_index.flip(0)), dim=1)
 
        x = self.input_conv(x, edge_index)
        x = F.relu(x)
        x = self.hidden_conv1(x, edge_index)
        x = F.relu(x)
        x = self.hidden_conv2(x, edge_index)
        return x

But this totally fails. I then backed things off a a bit to an even simpler case. If that doesn’t work, then perhaps a hardcoded 3 body problem would:

Fully connected MLP

So I put together this. Obviously it would not generalise to more particles, but nonetheless you would think it would works as a hardcoded example. No, though. it’s terrible.

class NbodyManual(torch.nn.Module):
    def __init__(self, num_features: int):
        super().__init__()
        hidden_size = 500
        self.input_conv = Linear(num_features, hidden_size)
        self.hidden_conv1 = Linear(hidden_size, hidden_size)
        self.hidden_conv2 = Linear(hidden_size, hidden_size)
        self.output_conv = Linear(hidden_size, num_features) 
    def forward(self, x):
        orig_shape = x.shape
        if x.ndim == 2:
            x = x.flatten()
        else:
            x = x.reshape(x.shape[0], -1)
        x = self.input_conv(x)
        x = F.relu(x)
        x = self.hidden_conv1(x)
        x = F.relu(x)
        x = self.hidden_conv2(x)
        x = F.relu(x)
        x = self.output_conv(x)
        return x.reshape(orig_shape)

Here is what it looks like: Yuck. The way that I trained things was by generating 10e3 trajectories of 1e3 timesteps each, and then randomly sampling from these at training time. For the MLP I also used a batch size of 1000 and learning rate of 3e-4. I messed about for many of these parameters but nothing changed anything. Even having fewer layers didn’t.

Go simpler - y = x**2

Here is a neural net that is trying to do y = x**2:

    class Net(torch.nn.Module):
        def __init__(self):
            super().__init__()
            hidden_size = 10
            self.input_conv = Linear(1, hidden_size)
            self.hidden_conv = Linear(hidden_size, hidden_size)
            self.output_conv = Linear(hidden_size, 1) 
            self.act = LeakyReLU()
        def forward(self, x):
            x = self.act(self.input_conv(x))
            x = self.act(self.hidden_conv(x))
            x = self.output_conv(x)
            return x

And here are the training results: 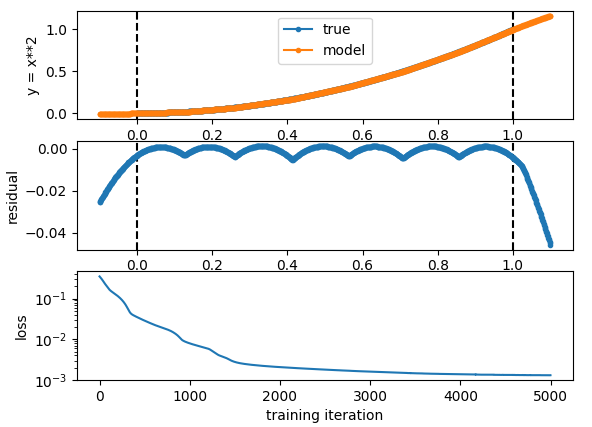Here the vertical line denotes the limits of the training data. It’s pretty clear from looking at the residual that the output is a piecewise linear approximation of the input. This is all very well and good but as expected it generalises super poorly outside the training distribution, which we can also see. The reason that this is the case is of course that multiplications + relu cannot take the input of a neural net and multiply it by itself - This would enable it to learn the true function being approximated here. When simulating physics and stuff there are many types of relationships (like gravitation) where the relationship is a very simple one when expressed as multiplications and whatnot. But something like this can really only do linear approximations, and so it will never generalise very well. It’s been pointed out to me that one of the things you can do here is perform various interesting functions, x**n, sin(x), exp(x) etc etc as inputs to the net so that it can learn how they work.

The bitter lesson

The bitter lesson is that all attempts to add human knowlege into the system are irrelevent compared to adding moar weights. The question is whether or not adding these fancy functions as inputs counts as this kind of optimisation. I suspect this comes down to how easy they are to approximate in practice. If you can do the job of an exp(x) with another layer or two it won’t matter. But if you can’t, then it does matter. Another problem with such things are exploding gradients. 1/x, exp(x) etc etc all have this habit of going to infinity. Some very initial results here suggest that this is going to be a problem, since the opposite of the vanishing gradient problem will occur. The optimiser will spend all its time making sure that the exponential doesn’t so anything funny and output 1e12 all of a sudden that it cannot actually approximate the desired function.

Small experiments adding spiciness

Adding x**2 to the input of the “mlp” so all it has to do is select the right input gives us this:

    class Net(torch.nn.Module):
        def __init__(self):
            super().__init__()
            hidden_size = 1
            self.input_conv = Linear(2, hidden_size)
            self.output_conv = Linear(hidden_size, 1) 
            self.act = ReLU()
        def forward(self, x):
            x = torch.cat((x, x**2), dim=1)
            x = self.act(self.input_conv(x))
            x = self.output_conv(x)
            return x

And here is the result: 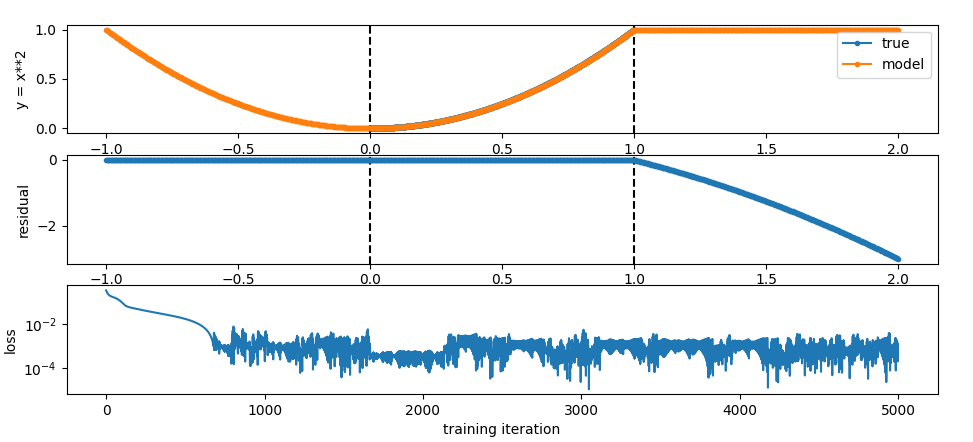So if you constrain stuff enough, things do generalise but of course the model has no way to know that the Relu kicking in one the right hand side will cause things not to work when it generalises.

Muddying the waters

Here is what happens when I add an exp(x) as an input to the network:

    class Net(torch.nn.Module):
        def __init__(self):
            super().__init__()
            hidden_size = 3
            self.input_conv = Linear(3, hidden_size)
            self.output_conv = Linear(hidden_size, 1) 
            self.act = ReLU()
        def forward(self, x):
            x = torch.cat((x, x**2, torch.exp(x)), dim=1)
            x = self.act(self.input_conv(x))
            x = self.output_conv(x)
            return x

Note that I also messed about with the hidden size etc to get the result that I wanted, as is standard practice for ML. Here is the result: 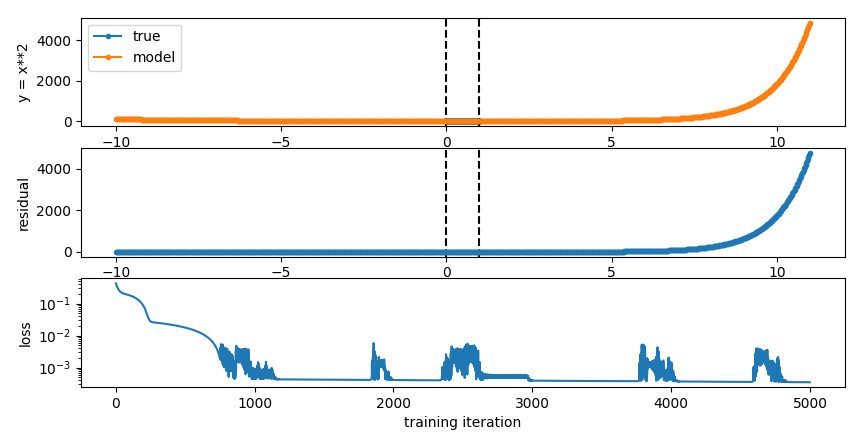we can see that the loss absolutely explodes after a little bit. This is the effect I was looking for before and I think it will mean that adding this kind of stuff will cause problems.

Inverse

Here are the results of trying to simulate this:

    def fn(x): return 1 / (1e-3 + x**2)

With an x2 available on the input: 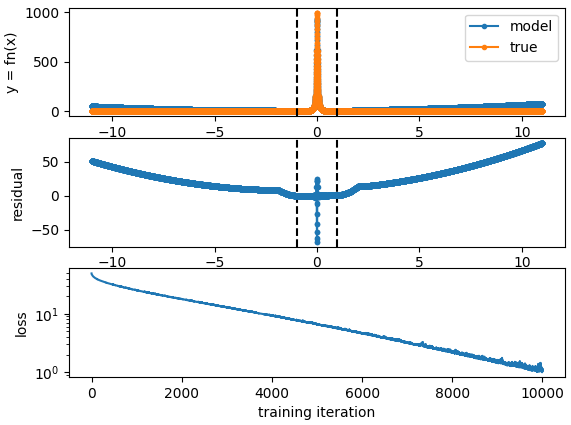without: 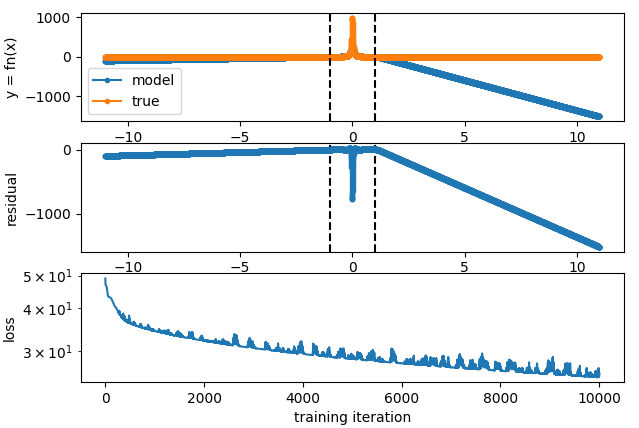without, but with a single hidden layer: 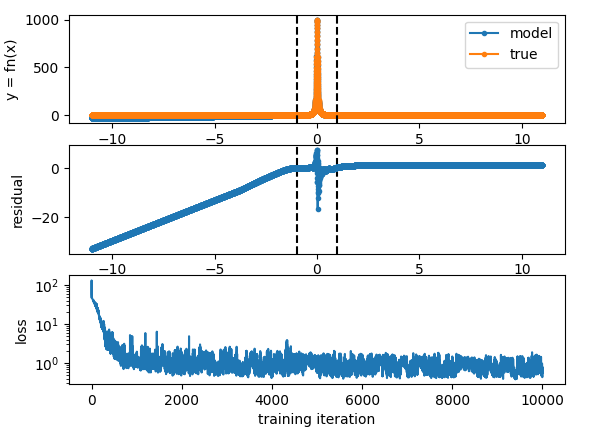I suppose this experiment is a point in favour of the universal approximation theorum.