N body simulation: Basics
We all know this, right? Here it is implemented in pytorch in a batched fashion:
# def n_body_step(state: torch.Tensor, G: float = 6.674e-11, dt: float = 1e-3):
def n_body_step(state: torch.Tensor, G: float = 10, dt: float = TIMESTEP):
add_batch_dim = True if len(state.shape) == 2 else False
if add_batch_dim:
state = state.unsqueeze(0)
assert len(state.shape) == 3
assert state.shape[-1] == NUM_STATES
# state is a B * N * 5 batched tensor of masses, positions, and velocities.
# dt is the time step
N = state.shape[1]
x_diff = (state[:, :, X_IDX].unsqueeze(-2) - state[:, :, X_IDX].unsqueeze(-1)) # B * N * N
y_diff = (state[:, :, Y_IDX].unsqueeze(-2) - state[:, :, Y_IDX].unsqueeze(-1)) # B * N * N
x_diff_sq = x_diff ** 2 # B * N * N
y_diff_sq = y_diff ** 2 # B * N * N
range_ = torch.sqrt(x_diff_sq + y_diff_sq)
inv_range_sq = 1 / (x_diff_sq + y_diff_sq)
# mask out self-interactions without using multiplication because that gives nans:
inv_range_sq = inv_range_sq.masked_fill(torch.eye(N, dtype=torch.bool), 0)
accel_mag = 0.5 * G * state[:, :, M_IDX].unsqueeze(-1) * inv_range_sq
# We need to find the direction of the acceleration:
direction_vec = torch.stack([
(x_diff / range_),
(y_diff / range_),
], dim=1) # 2 * N * N
direction_vec = direction_vec.masked_fill(torch.eye(N, dtype=torch.bool).unsqueeze(0).unsqueeze(0), 0)
accel = accel_mag.unsqueeze(1) * direction_vec
accel = accel.sum(dim=-2) # B * 2 * N
accel = -accel.transpose(-1, -2) # B * N * 2
# update velocities:
state[:, :, 3:5] += dt * accel
# update positions:
state[:, :, 1:3] += dt * state[:, :, 3:5]
state[:, :, 5:7] = accel
if add_batch_dim:
state = state.squeeze(0)
return stateThis works pretty well, apart from the one small problem that when two objects are close together terrible floating point things happen and they fly off. I figure instead of doing this they should seamlessly pass through each other when interacting. To do this I calculate whether or not the distance from one object to another is comparable to the amount that it would be accelerated by in one timestep. If it is, then the acceleration should be 0 instead. Here is the accelleration code:
# Derate the acceleration if the objects are too close:
expected_movement = (0.5 * accel_mag * dt ** 2) / (1e-9 + range_)
accel_derating = 1/(torch.exp((100 * expected_movement)**2))
accel_mag *= accel_deratingWhich looks like this if you plot it:
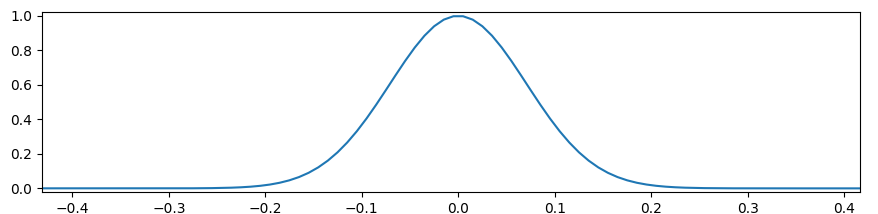
Results
Here is a visualisation (Thanks ChatGPT) of what the population statistics look like before this derating is put in:
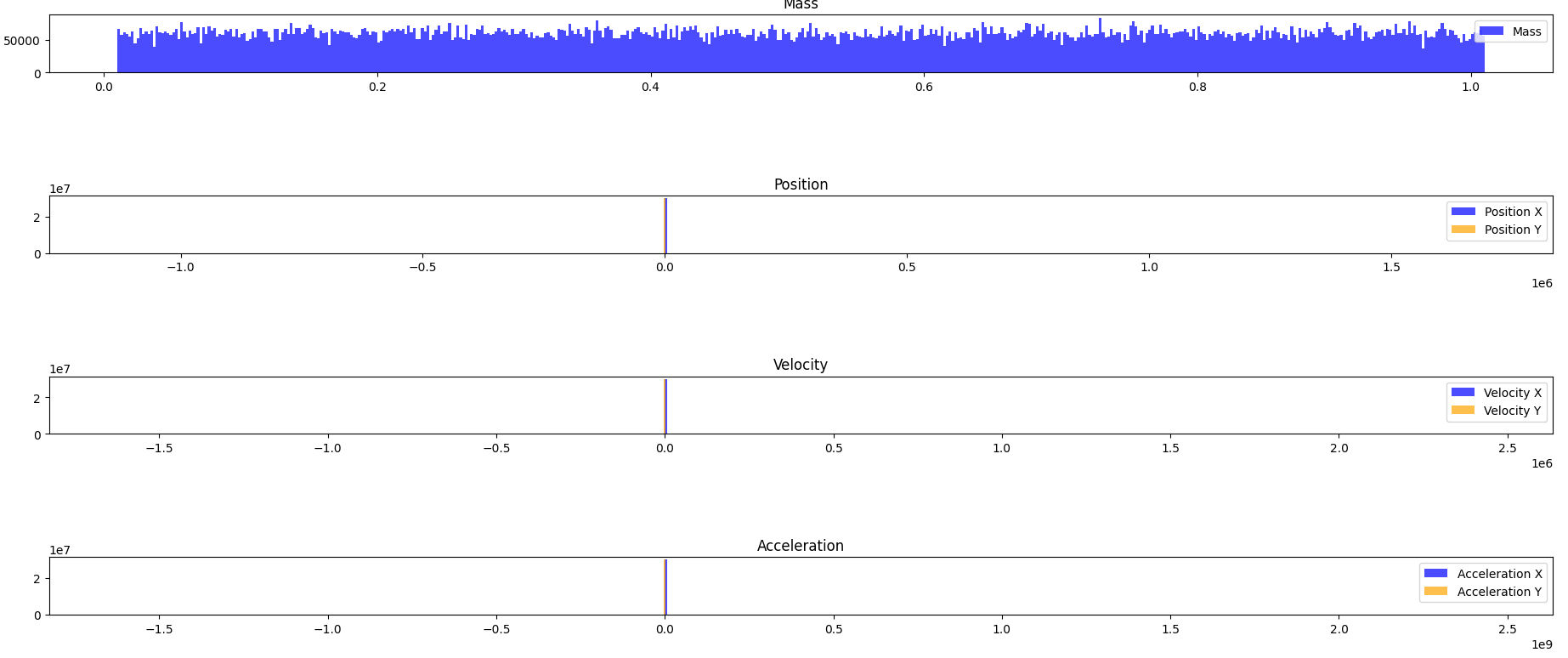 And after:
And after:
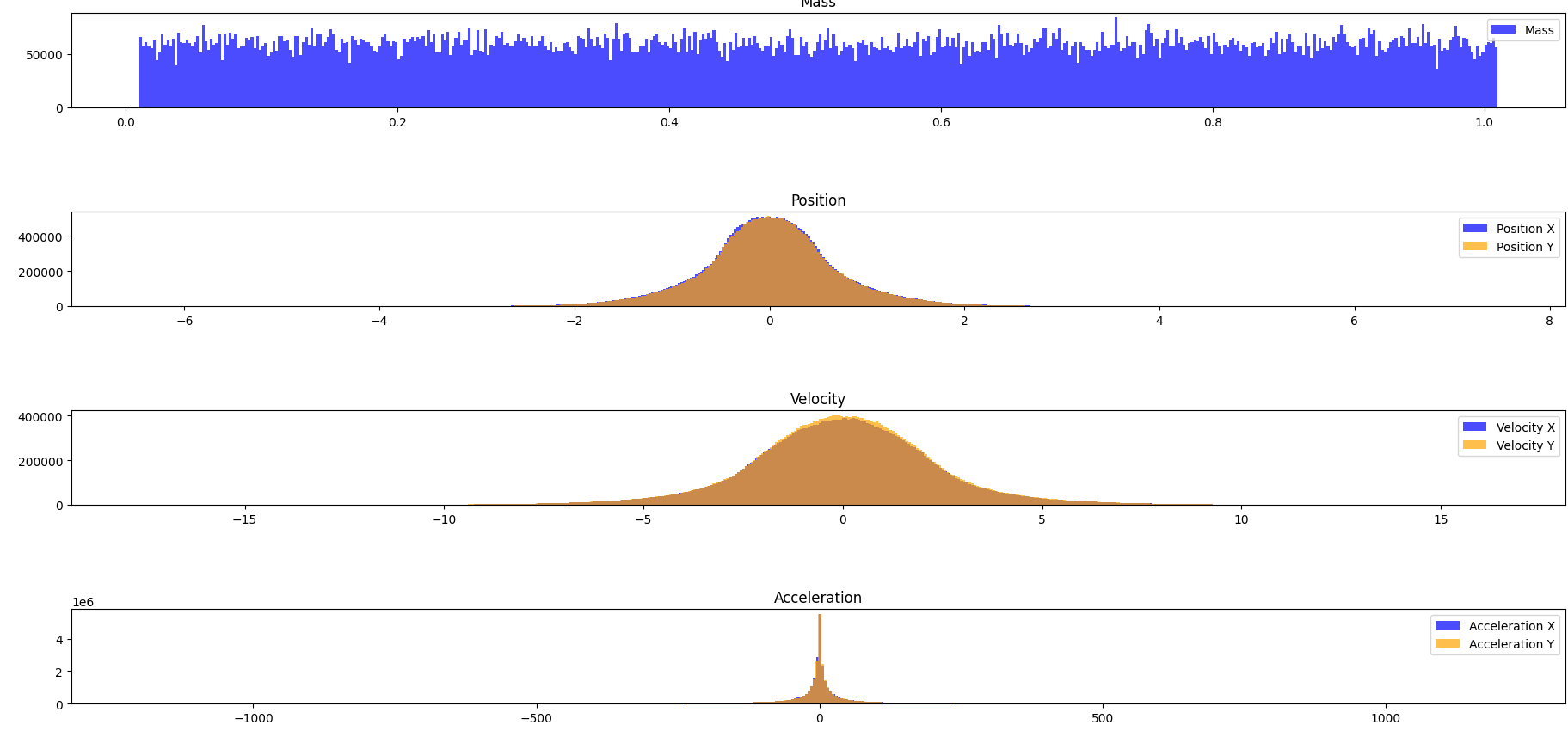 Rather dramatic, wouldn’t you say?
This seems to have a fairly large effect on training, especially if you use something like a mean squared error loss, like I was.
Rather dramatic, wouldn’t you say?
This seems to have a fairly large effect on training, especially if you use something like a mean squared error loss, like I was.
Small aside: fiddling with this made the simulation look a lot better:
Noisy noisy results
Here are the results trianing for a bit with a batch size of 1, using L1 loss:
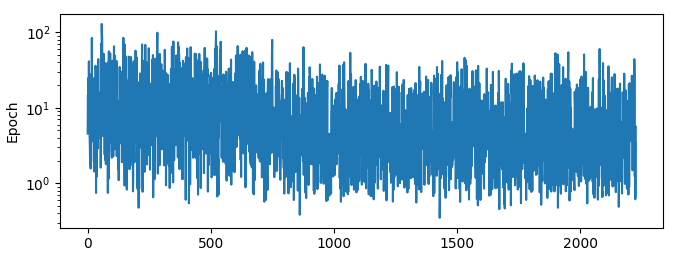 2+ orders of magnitude differences in the error rates seems kinda high, no? When I use a batch size of 1000, I get this:
2+ orders of magnitude differences in the error rates seems kinda high, no? When I use a batch size of 1000, I get this:
 Which looks significantly more intelligble to me. There is a paper which I have read all the way through and downloaded the source code for etc, and one of the things that they did was actually train the net to predict only the accelerations, then use a simple to actually calculate the positions. This intuitively makes sense here because it is indeed the forces on the particles that we are actually trying to calculate, but it also does not make sense to me because if you look at the statistics of the accelerations above, the acceleration is extremely high variance. Maybe we should try and predict the log of the acceleration?
Here is the training loss predicting acceleration with L1 loss (note x axis):
Which looks significantly more intelligble to me. There is a paper which I have read all the way through and downloaded the source code for etc, and one of the things that they did was actually train the net to predict only the accelerations, then use a simple to actually calculate the positions. This intuitively makes sense here because it is indeed the forces on the particles that we are actually trying to calculate, but it also does not make sense to me because if you look at the statistics of the accelerations above, the acceleration is extremely high variance. Maybe we should try and predict the log of the acceleration?
Here is the training loss predicting acceleration with L1 loss (note x axis):
 …Not very good, as you might think.
…Not very good, as you might think.
Predicting log(acceleration)
Let’s make the net try to predict log2(accel.abs() + 1). The augmentation looks like this:
timesteps = torch.randint(0, num_timesteps - 1, (batch_size,))
trajectories = torch.randint(0, num_trajectories, (batch_size,))
data_start = dataset[timesteps, trajectories, :, :].squeeze().clone()
data_end = dataset[timesteps + 1, trajectories, :, :].squeeze().clone()
data_start[:, :, -2:] = torch.log2(data_start[:, :, -2:].abs() + 1)
data_end[:, :, -2:] = torch.log2(data_end[:, :, -2:].abs() + 1)
out = model(data_start)
loss = F.l1_loss(out[-2:], data_end[-2:])The histogram looks like this:
 Which seems wayyyy nicer.
The results looks like this:
Which seems wayyyy nicer.
The results looks like this:
 …Which seems a bit better, maybe? It obviously trained a bunch more but we are kinda taking the log of the loss here, so I’m not that impressed. It does seem to be learning though so bumping up the batch size to 10k we get this:
…Which seems a bit better, maybe? It obviously trained a bunch more but we are kinda taking the log of the loss here, so I’m not that impressed. It does seem to be learning though so bumping up the batch size to 10k we get this:
 …Doesn’t seem to be much gain from increasing the batch size 10x.
…Doesn’t seem to be much gain from increasing the batch size 10x.
Sanity check: Cheat
Perhaps the reason this is all going so poorly is there is some kind of horrific bug. Perhaps I have forgotten to torch.zero_grad? or switched the desired and predicted in the loss? So to see if that is the case, I concatenated the desired state as an input to the net to see if it could learn to do a passthrough OK.
def forward(self, x):
orig_shape = x.shape
x_next = nbody.n_body_step(x) # calculate the desired state
x = x.reshape(x.shape[0], -1)
x_next = x_next.reshape(x.shape)
x = torch.cat([x, x_next], dim=-1) # Add the desired output to input
x = self.act(self.input_conv(x)) # All this nonsens just has to do a passthrough.
x = self.act(self.hidden_conv1(x))
x = self.act(self.hidden_conv2(x))
x = self.output_conv(x)
return x.reshape(orig_shape)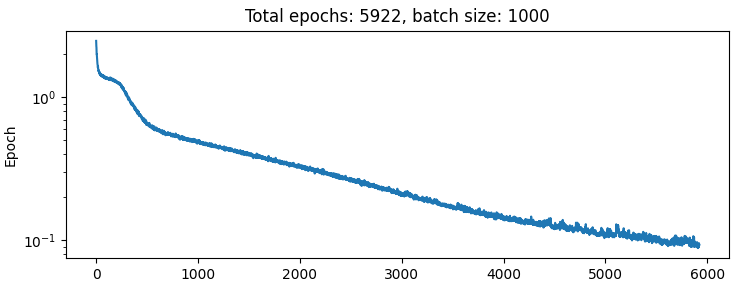 …So that’s not the problem, then.
…So that’s not the problem, then.
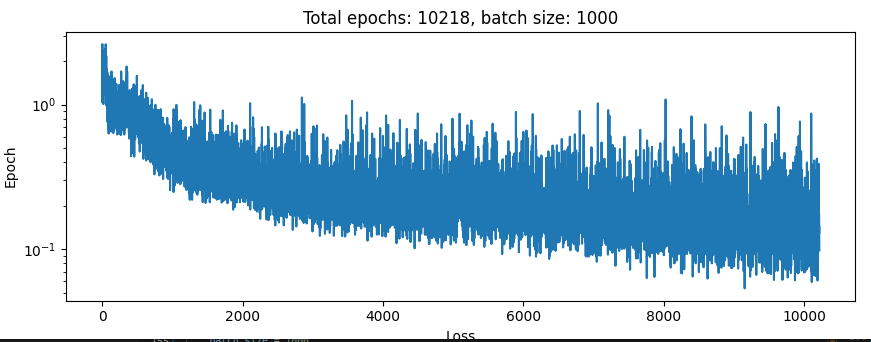
”Quick” experiment: maybe we just need more flops?
Everyone knows that nets take lots of compute to train. So I trained this net:
class NbodyManual(torch.nn.Module):
def __init__(self, num_features: int):
super().__init__()
hidden_size = 100
expansion = 2
self.input_conv = Linear(num_features * expansion, hidden_size)
self.hidden_conv1 = Linear(hidden_size, hidden_size)
self.hidden_conv2 = Linear(hidden_size, hidden_size)
self.output_conv = Linear(hidden_size, num_features)
self.act = ReLU()
def forward(self, x):
orig_shape = x.shape
if x.ndim == 2:
x_next = nbody.n_body_step(x.clone())
x = x.flatten()
x_next = x_next.reshape(x.shape)
else:
x_next = nbody.n_body_step(x.clone())
x = x.reshape(x.shape[0], -1)
x_next = x_next.reshape(x.shape)
x = torch.cat([x, x_next], dim=-1)
x = self.act(self.input_conv(x))
x = self.act(self.hidden_conv1(x))
x = self.act(self.hidden_conv2(x))
x = self.output_conv(x)
return x.reshape(orig_shape)For a bit over a day and got 25e6 epoches with a batch size of 1000. So 1e10 forwards passes of the net, which took about 24 hours. Learning rate of 3-e4, naturally. Here is what the loss function looks like:
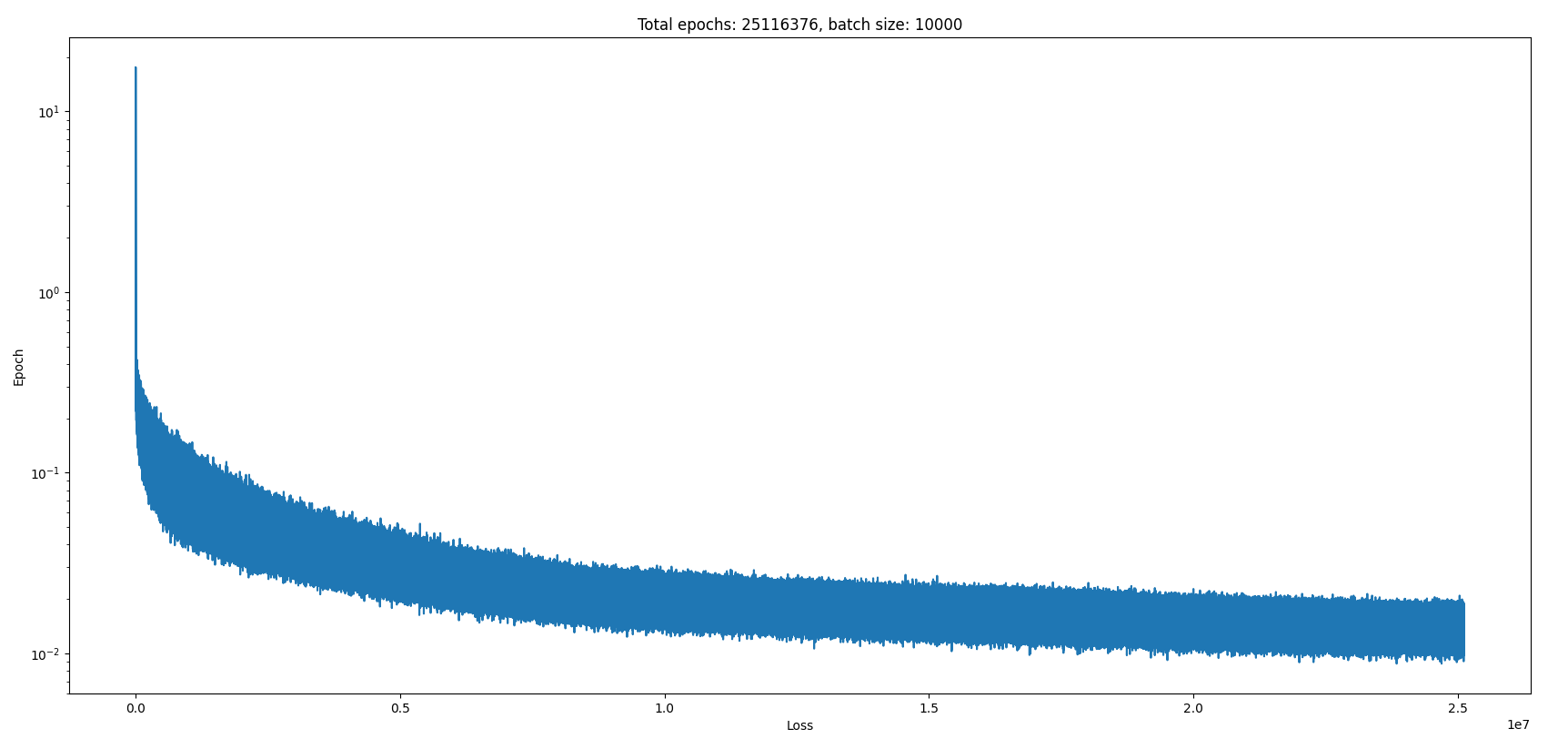 So it was still improving the whole time!
That’s impressive and noteworthy. Notice something about the model though? I concatenated the expected output onto the input, so all it had to do was learn to pass it through, and it didn’t even seem to be that good at doing that!
Here is what it looks like against the ground truth:
I can’t escape the feeling that something is subtly wrong here. There’s no way that this can be that bad, I must be missing something. Recalling this blog post neural net bugs often look like performance that’s just a little bit worse. But that’s why I did this, so that I could verify that I had no such obvious bugs.
So it was still improving the whole time!
That’s impressive and noteworthy. Notice something about the model though? I concatenated the expected output onto the input, so all it had to do was learn to pass it through, and it didn’t even seem to be that good at doing that!
Here is what it looks like against the ground truth:
I can’t escape the feeling that something is subtly wrong here. There’s no way that this can be that bad, I must be missing something. Recalling this blog post neural net bugs often look like performance that’s just a little bit worse. But that’s why I did this, so that I could verify that I had no such obvious bugs.
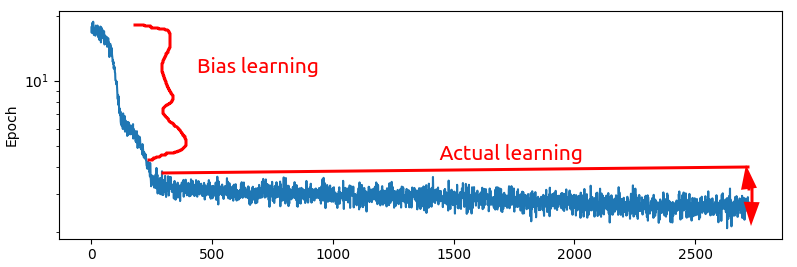
Quick aside: Loss functions that go up again:
Here is the result of training the net on an input of [x, x_next] so all it has to learn is to do a passthrough of the second half of the net:
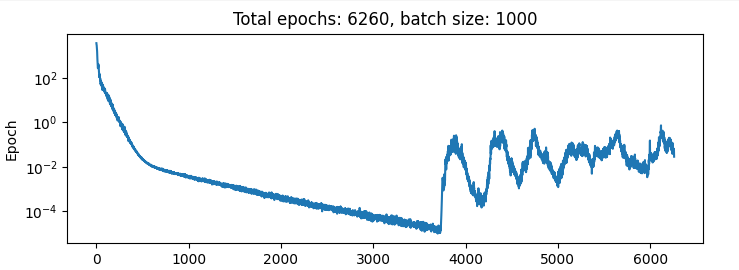 Why does the loss function jump up to such a high result after a while???? what’s going on here? This seems important. I hear that the adam optimiser has some momentum, maybe that caused it to overshoot and then for some reason it can’t get back again? so weird.
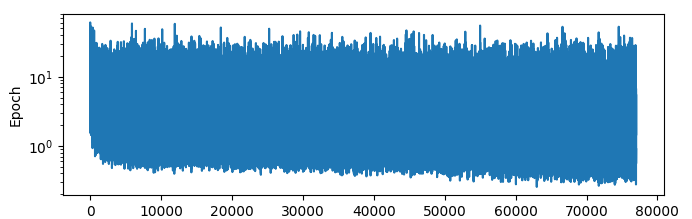
This is what happens when I decrease the learning rate by a factor of 10 to 3e-5:
Why does the loss function jump up to such a high result after a while???? what’s going on here? This seems important. I hear that the adam optimiser has some momentum, maybe that caused it to overshoot and then for some reason it can’t get back again? so weird.
This is what happens when I decrease the learning rate by a factor of 10 to 3e-5:
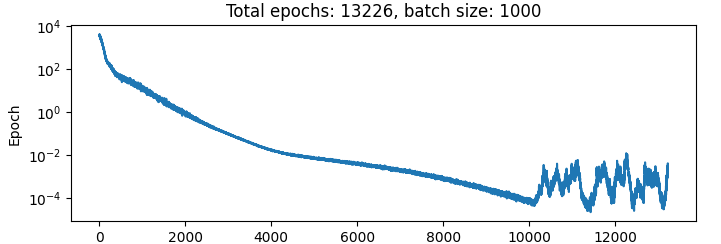 So it doesn’t looks like a learning rate problem.
So it doesn’t looks like a learning rate problem.
Loss statistics
We have looked at the state statistics before, but what about the loss statistics? Here are the L1 and mse losses for a single step of the simulation:
states = states.re`shape(-1, states.shape[-2], states.shape[-1])
states_next = nbody.n_body_step(states.clone())
l1 = (states - states_next).abs().mean(dim=(-1, -2)).cpu().detach().numpy()
mse = ((states - states_next)**2).mean(dim=(-1, -2)).cpu().detach().numpy()
l1 = np.log10(l1); mse = np.log10(mse) And if you don’t include the acceleration:
And if you don’t include the acceleration:
