20230610 N body again

Previously, on NN adventures: I figured out that optimising the ratio of the input to the output was what was needed. Let’s use that information and go back to training N body simulations. Taking the Exact same loss function and whacking it into the N body training loop (the one where we are just trying to pass the input to the output), the loss looks like this: 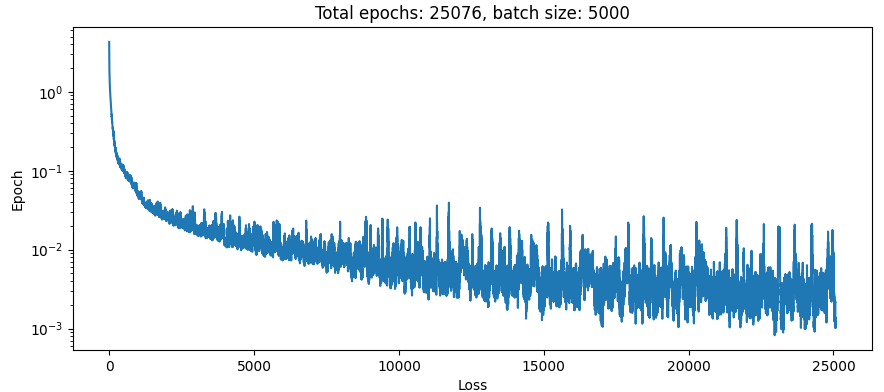Not great. Stuff just flies around in the sim as per usual, too. Looks like the learning rate is too high though. Changing things so there is only one hidden layer and reducing the learning rate to 3e-5 and I get this: 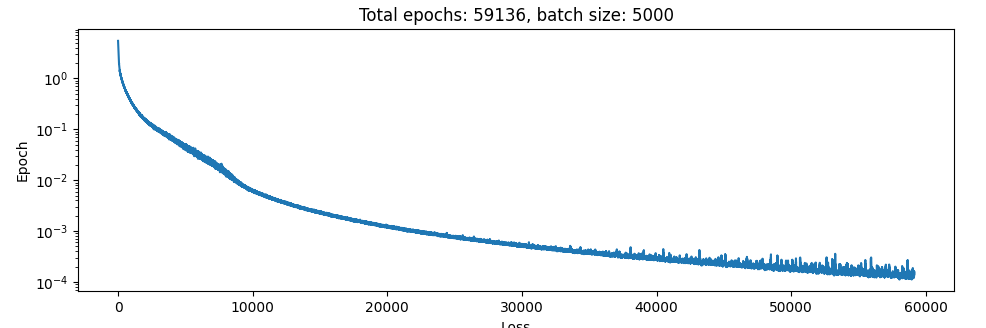…Now that’s more promising. But no, stuff just flies around in the simulator as per normal. I think I could do with a scheduler here. That took quite a few minutes to train, and at the end there it looked like the learning rate was still too high. Here’s the scheduler:

    batch_size = 5000
    oom_decay = 3
    epochs = 10000
    learning_rate_start = 1e-2
    optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate_start)
    scheduler = ExponentialLR(optimizer, gamma=np.power(10, -oom_decay / epochs))

And the results: 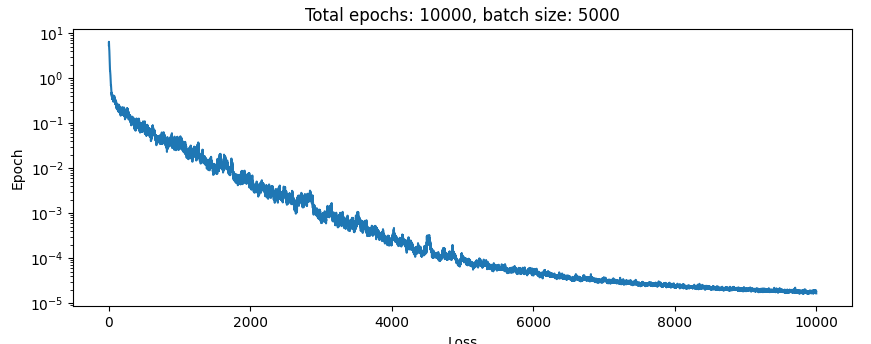Boom. 2 OOM improvement in the loss with 1/6 the training time. Noice. In the simulation we can actually see that the bodies kind of interact with each other. I noticed in the above graph things kinda slowed down a bunch at the end there, so trained for 10x longer with the same scheduler. And I got this: 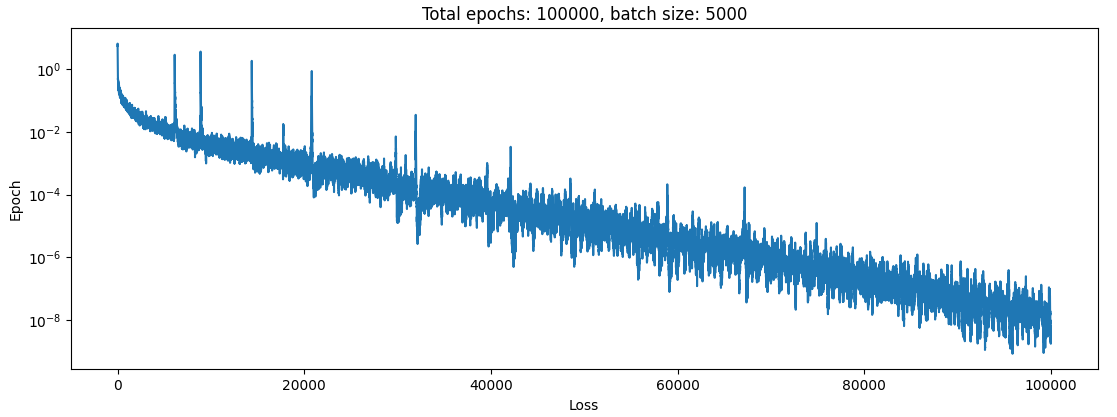HMMMMMM. That is some nice perfectly scheduled learning right there (I think). Another 3 OOM improvement. Let’s take a look in the simulator: !!! Finally. Some modicum of success. Time to remove the output from the input lol.

A note on training speed.

It look 100e3 iterations of a batch size of 4e3 for this model with like 1000 parameters in it to learn the identity function. This really really does not bode well for learning anything more complex with short development cycles.

First results with new fitness function:

Here is what happens training over 1e6 iterations using a learning rate decaying from 1e-3→1e-6: 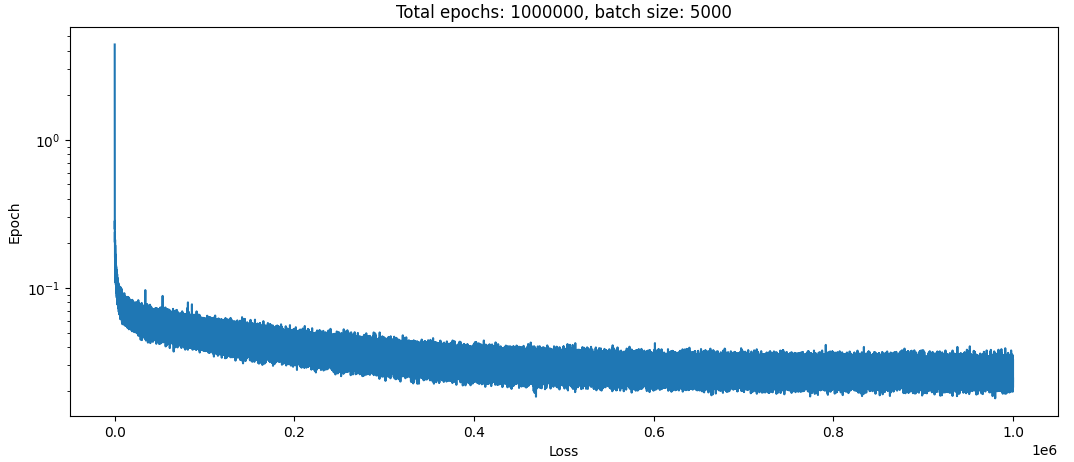…Yep, not great. This is quite similar to what I got before really (note of course that the absolute magnitude of the loss here is not comparable).

Gradient speed

Maybe what’s going on here is that although we are optimising for the right thing here (percentage error) we are doing so in a way that produces a super weak gradient on account of the log. This is a bit of a incoherent notion that I don’t really understand.

If the gradient is weak, why not just multiply it by a higher learning rate? Perhaps because the variance in the model is not correspondingly weak, and so the signal to noise ratio is poor here?
If we have a fitness function with a stronger gradient, isn’t that basically the same as going back to mean squared error again? Is it a linear thing between “correct fitness function that takes ratio but gives weak signal” and “strong fitness function that gives good signal but prioritises fixing spiky bits in the loss landscape at the expense of everything else”, or are the two independent and we can find a function that performs well one both accounts? I don’t really know what if any of these things are true. Maybe this is where one of those literature searches would be good. One of my favourite papers “Learning to simulate complex physics with graph neural networks” has this to say on the topic: They were doing fluid simulations and suchlike. I think though that what they were doing might actually be a bit easier than this though. Intuitively I would expect the dynamic range of the problem to be quite a bit lower. Water particles only interact with what’s right next to them and do so with a (relatively) low range of forces. So they might have just not run into this problem.

Quick replication attempt.

here is a paper that does the three body problem - exactly the same as what I have been trying to do. Prolly should have looked this up earlier but oh well. Their structure is also super simple - a 128 wide by 10 deep MLP. let’s whack that into pytorch and see how it goes. Here is the loss function: 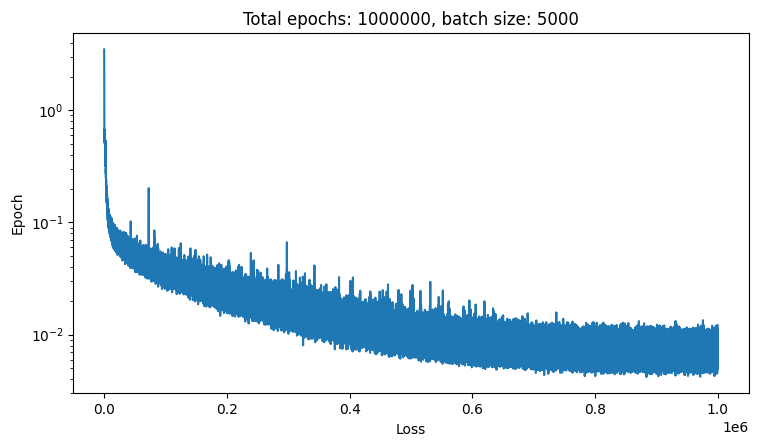Gyarbage! We know from above that you need like 1e-6→1e-8 loss to get good results, this isn’t even close to that. I’m getting pretty strong “dataset is high variance and that’s why it isn’t training” vibes from that loss function too.

Next steps

So from here I can:

Fudge the N body simulation so that it’s smoother, akin to having an epsilon of 1e-2 [[20230610 inv x squared a deep dive#Background#Experiments varying epsilon| like this]] to see if it makes things easier to train. This will verify that it’s the spikyness that is what’s causing the issue.
Try to find a better loss function, since I got such great improvements from that route already
Train on a tiny subset of the data to try to overfit, and then generalize from there.

The last option is easiest, so let’s try that next:

Train on 10 timesteps of one simulation.

Here is the loss curve for training on 10 simulation steps of a single initial state only: 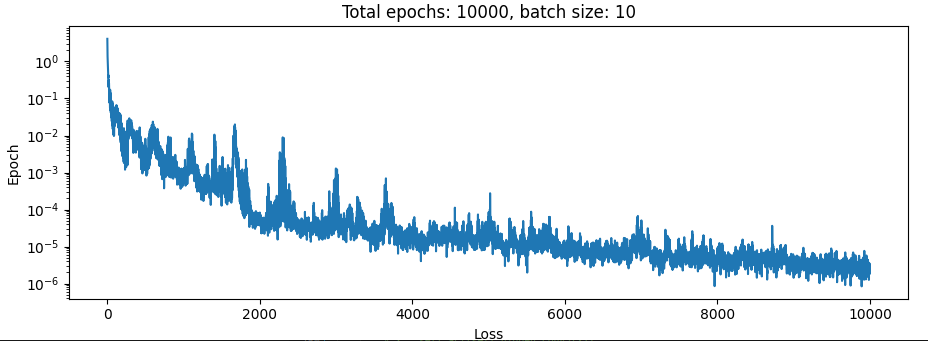So that seems somewhat reasonable. Let’s bump it up to 10 trajectories each with 10 simulation steps: 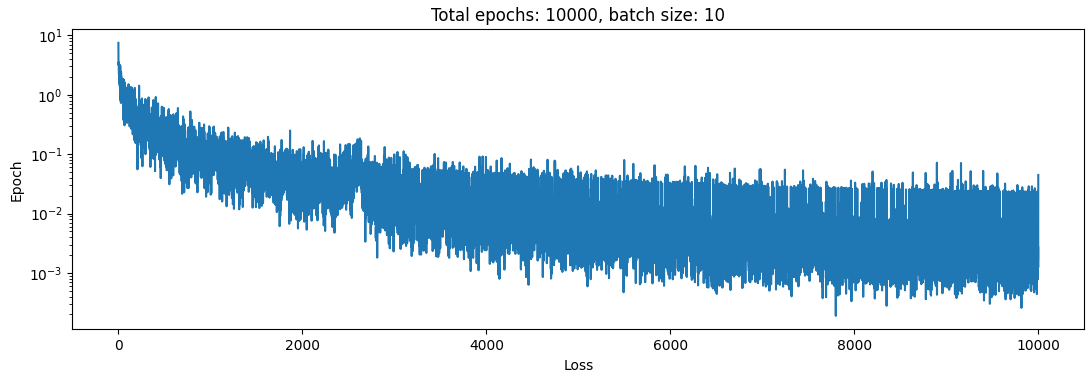So we can see that already that’s enough to cook the loss!

Train with a different fitness function.

I updated the fitness function to the one here, and then trained it on the 128 wide 10 deep architecture from before for about 8 hours with a learning rate decaying from 3e-3 to 2e-6. Dataset was two bodies this time, 50e3 trajectories of 1000 timesteps each. Here are the results: 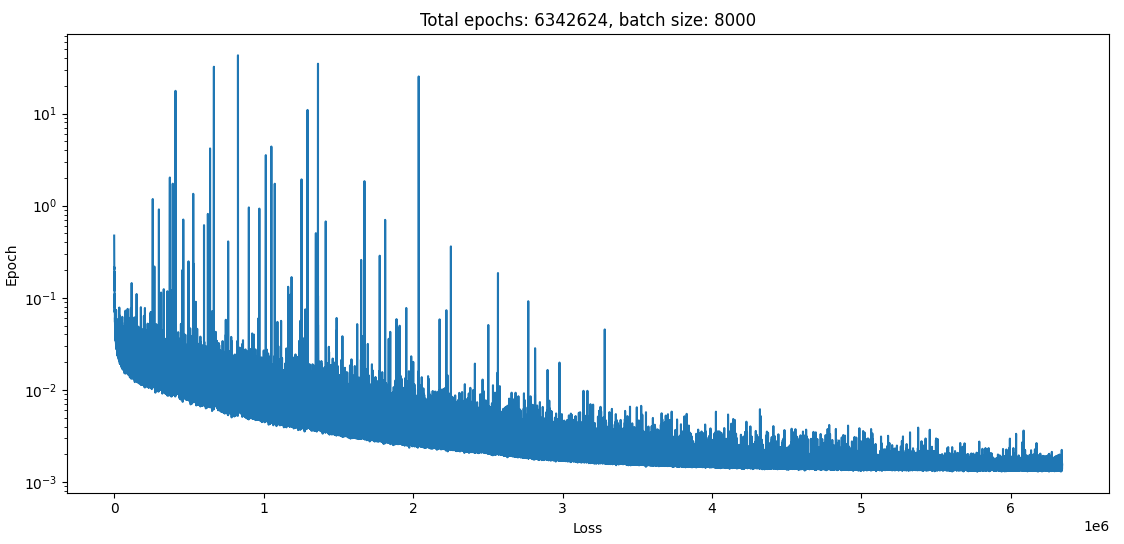well, it seems to have converged on something… Let’s check it out in the sim: It verks! Incredible. It doesn’t work that well, but it does recognisably solve the problem. Amazing. Only took like a month. Now to do the same thing, but with three bodies. And here are the results for that: 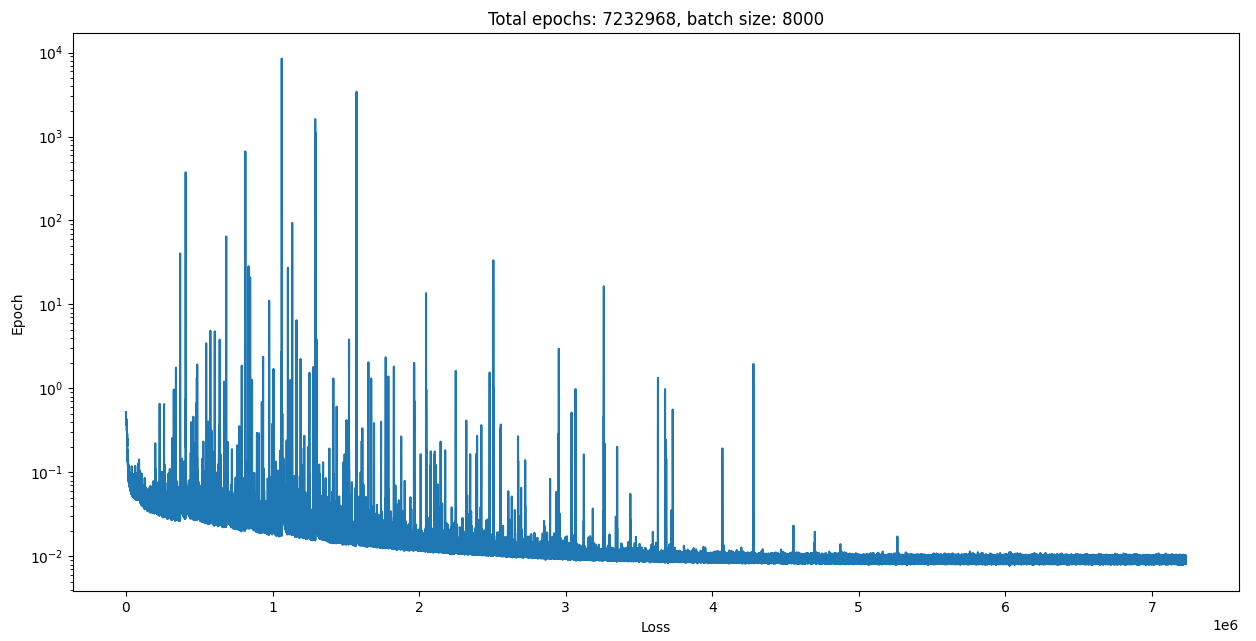…Seems to converge with an error about 10x higher, oh well. Let’s zoom in on one of these spikes of error: 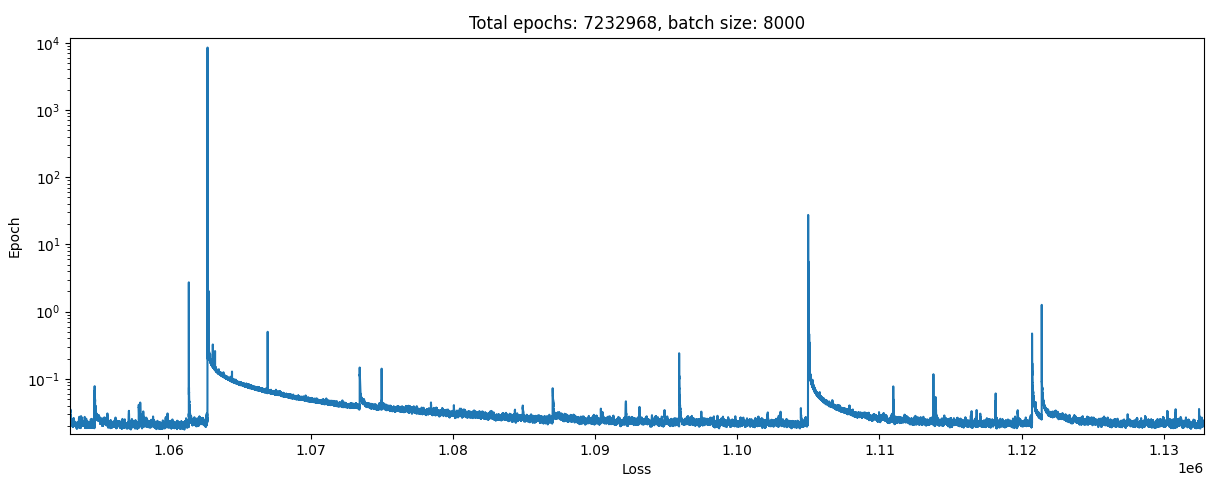so it looks like the model sometimes gets updated in a very poor direction, then has to spend a long time recovering from this before it has a chance to get back to where it was. Even though the batch size is like 8000, I suspect that the cause of this is one example within the batch having a truly stupendous error that throws everything out. I guess this could be from two causes:

Early in the training process the model has not adapted well, and so occasionally guesses very wrong.
Early in the training process the learning rate is high, so the model weights get thrown into a bad area of the loss function. The latter sounds more likely to me. If this is the failure mode of the model however, one thing that we could do is do something like

for epoch in range(num_epochs):
	model(data)...blah blah train
	if(curr_loss > prev_loss * 10): continue

This might be a good idea but I think it is also papering over the issue. Before I go and do something like that we should go and understand in great and excruciating detail why it is that everything is so profoundly fat tailed. I think that this is most likely a lesson that will translate well into future efforts. For example if our ground truth is a simulation, maybe we can gradually increase the ‘peakiness’ of the training data as a function of time (i.e. gradually decrease epsilon like I did here) which might make things train faster. That seems like something that could generalise well. It also seems like something that could paint you into a corner where you could only train on data that could be smoothed in this way too. GPT tells me that this kind of thing is called ‘Curriculum learning’.

Quick experiment: batch normalisation.

Here is the result of the same 10 layer network, only the first 7 layers are batch norm: 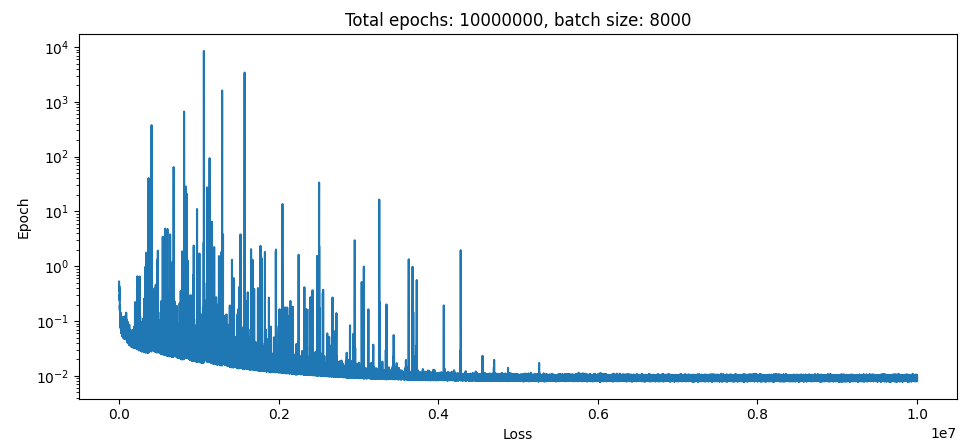basically exactly the same (take note of x axis).

Exploring the error

I set a breakpoint in vscode for when the error went up by more than a factor of 100, and got a breakpoint around 300e3. Here is what the ratio losses look like across the batch size of 8000: 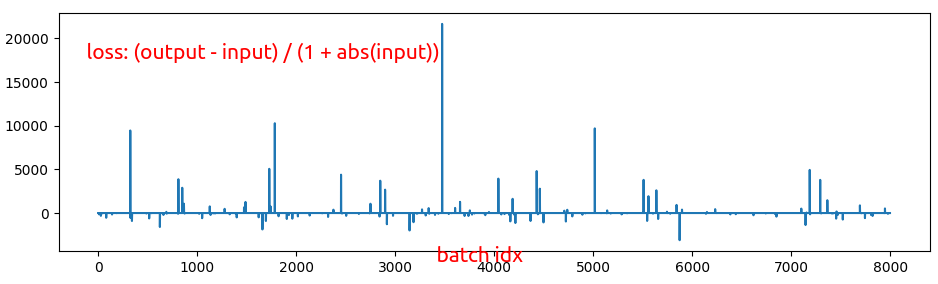What kind of absolutely atrocious distribution is that? Here are what things look like for the fitness function before that, the two sided log: well I’m not going to say that’s great, but it looks much better than the previous one. It’s clear with this too though that the loss is dominated by these outliers. inspecting them, they seem to be important as this is where the n bodies are undergoing high accelerations. Maybe if we optimised for the 0→95th percentile of losses this would work out better though and even though we would not be training on such extreme cases the model would still learn better. So many experiments!

Bringing the two training notions together

I have had two ideas about how to train these spiky functions:

Gradually increase the spikiness of the training data over time by increasing the epsilon in 1/x^2 or similar.
Reject some outlier losses to stop egregious model updates But don’t you see! Those are the same! If we we gradually update the weights over the training period from the 0th to 100th percentile of the losses, then it will by definition be learning on the easiest (smoothest) examples first! Someone must have thought of this already…

Results

Here is the loss curve from training in such a way that over the course of the training set the loss is calculated from a gradually increasing fraction of the errors, like so:

        def my_loss(target, pred):
            min_batch_ratio = 0.1
            percentile = (epoch / epochs) * (1 - min_batch_ratio) + min_batch_ratio
            ratio = (pred - target) / (1 + target.abs())
            ratio_batch = torch.mean(ratio, dim=(-1, -2))
            ratio_percentile = torch.quantile(torch.abs(ratio_batch), percentile)
            ratio_batch = ratio_batch[ratio_batch.abs() < ratio_percentile]
            return  ratio_batch.abs().mean()
        loss = F.l1_loss(my_loss(data_end, out), torch.zeros(1))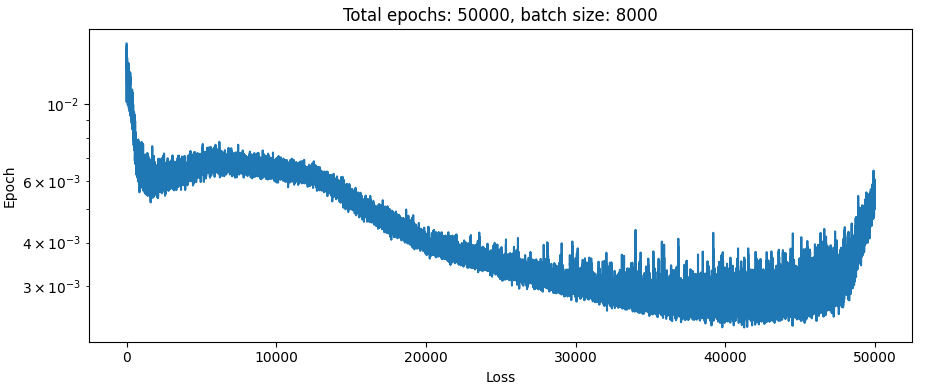

Well it certainly looks like something happened there. But in the simulation the bodies just fly apart. At least there were no spikes during training. Let’s take a look at what happens with the exact same setup and loss function, only difference is percentile is set to 1 always: 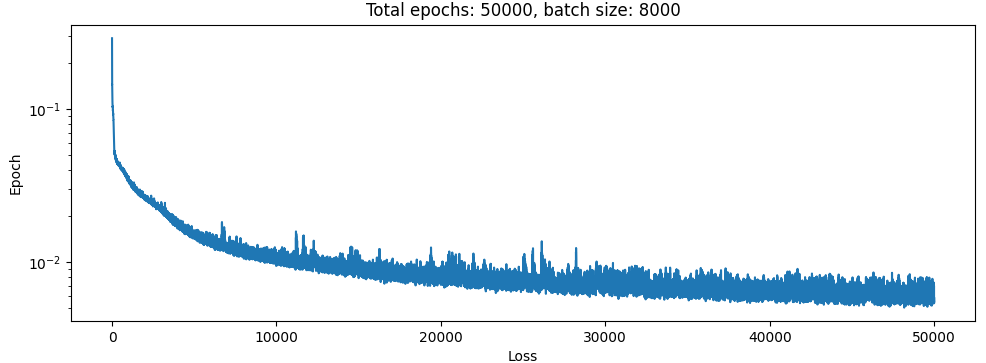I suppose this isn’t really valid since the first net never even trained at all on the hard examples really. So I changed the percentile calculation to this:

            min_batch_ratio = 0.1
            percentile = 2 * (epoch / epochs) * (1 - min_batch_ratio) + min_batch_ratio
            percentile = min(percentile, 1.0)

so that it would train on all the dataset for the last half of the training set. 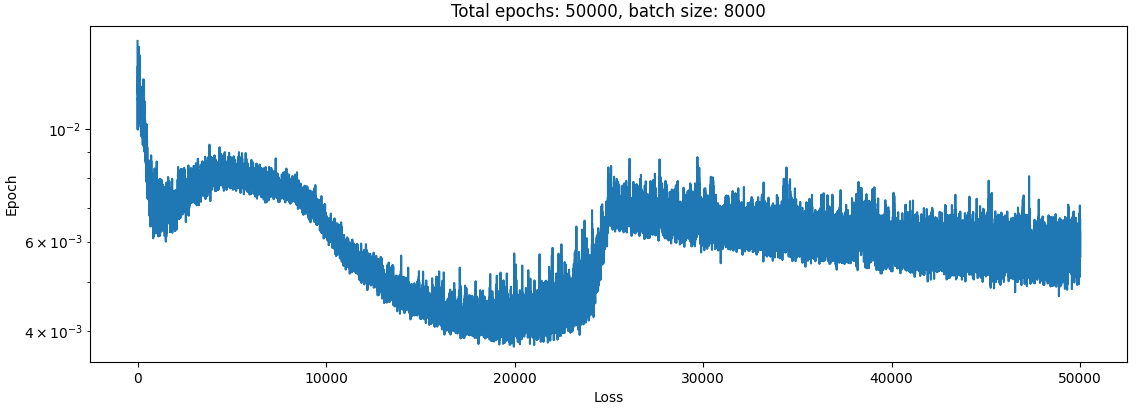So the final loss here is actually quite a bit better than the no-curriculum alternative, it looks like. The results in the simulation are a bit interesting, they looks like this:

What if we did the opposite?

Maybe the problem is not that the datset is super fat tailed, making it difficult to train on. Maybe the problem is that the training data is 99% “objects in motion stay in motion” and 1% “actual gravitation”. So what if we trained the net on a dataset where the bodies where experiencing high accelerations? Here is the result of training on the ~90th percentile examples with the highest accelerations (most newtons law, least “objects in motion”), learning rate decaying from 3e-3→3e-6. 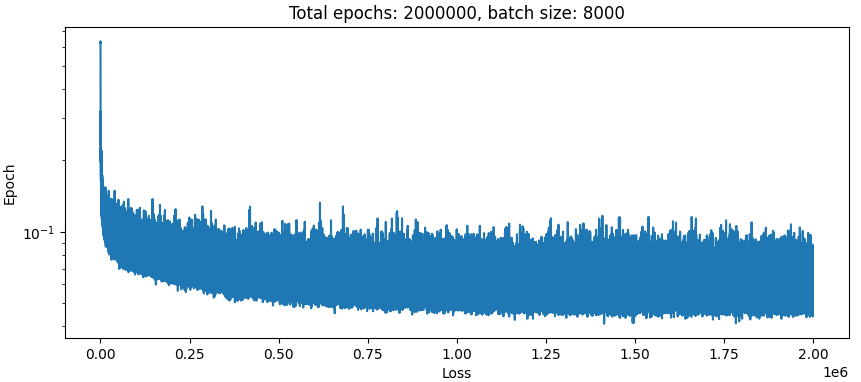more garbage. I think I’ll give up on nbodies for now, too hard. The whole thing was supposed to be a learning exercise anyway and I think it’s run its course there.

Quartz 4

Explorer