I am faffing about with the vesuvius challenge. At the moment this has been limited to getting chatGPT to generate me my very first autoencoder, which is a simple 3d convolutional model:
class Autoencoder(nn.Module):
def __init__(self, cube_size: int):
super(Autoencoder, self).__init__()
self.cube_size = cube_size
# Encoder
layers = 3
expansion_init = 32
self.encs = nn.ModuleList()
self.encs.append(nn.Conv3d(1, expansion_init, kernel_size=3, stride=1, padding=1))
for i in range(layers):
self.encs.append(nn.Conv3d(expansion_init * 2**i, expansion_init * 2**(i+1), kernel_size=3, stride=1, padding=1))
final_expansion = expansion_init * 2**layers
self.pool = nn.MaxPool3d(2, stride=2)
self.final_side_len = cube_size // 2**(layers + 1)
assert(self.final_side_len > 0)
self.final_channels = cube_size * 2**layers
self.final_paramcount = cube_size**3 // (2**(layers+1))
print(f"Final dimensionality before latent space will be {self.final_channels, self.final_side_len, self.final_side_len, self.final_side_len}")
latent_size = 512
# Latent vectors mu and logvar
self.fc1 = nn.Linear(self.final_paramcount, latent_size)
self.fc2 = nn.Linear(self.final_paramcount, latent_size)
# Decoder
self.dec1 = nn.Linear(latent_size, self.final_paramcount)
self.decs = nn.ModuleList()
for i in range(layers):
self.decs.append(nn.ConvTranspose3d(final_expansion // 2**i, final_expansion // 2**(i+1), kernel_size=2, stride=2))
self.decs.append(nn.ConvTranspose3d(final_expansion // 2**layers, 1, kernel_size=2, stride=2))
def reparameterize(self, mu, logvar):
std = logvar.mul(0.5).exp_()
eps = torch.randn(*mu.size())
return mu + std * eps
def encode(self, x):
for enc in self.encs:
x = F.relu(enc(x))
x = self.pool(x)
x = x.view(x.size(0), -1)
mu = self.fc1(x)
logvar = self.fc2(x)
return mu, logvar
def decode(self, z):
z = self.dec1(z)
z = z.view(z.size(0), self.final_channels, self.final_side_len, self.final_side_len, self.final_side_len)
d1, d2, d3, d4 = self.decs
z = F.relu(d1(z))
z = F.relu(d2(z))
z = F.relu(d3(z))
z = d4(z)
z = torch.sigmoid(z)
return z
def forward(self, x):
mu, logvar = self.encode(x)
z = self.reparameterize(mu, logvar)
decoded = self.decode(z)
return decoded, mu, logvar
# return self.decode(z), mu, logvar^^That’s the slightly upgraded variational version. What I have done is tr y to get it to reconstruct arbitrary 32**3 cubes of the scroll, picked from a ‘safe’ middle region:
In the future if I ever get anywhere with this I can do proper masking of where the scroll actually is.
Here is what the results look like:
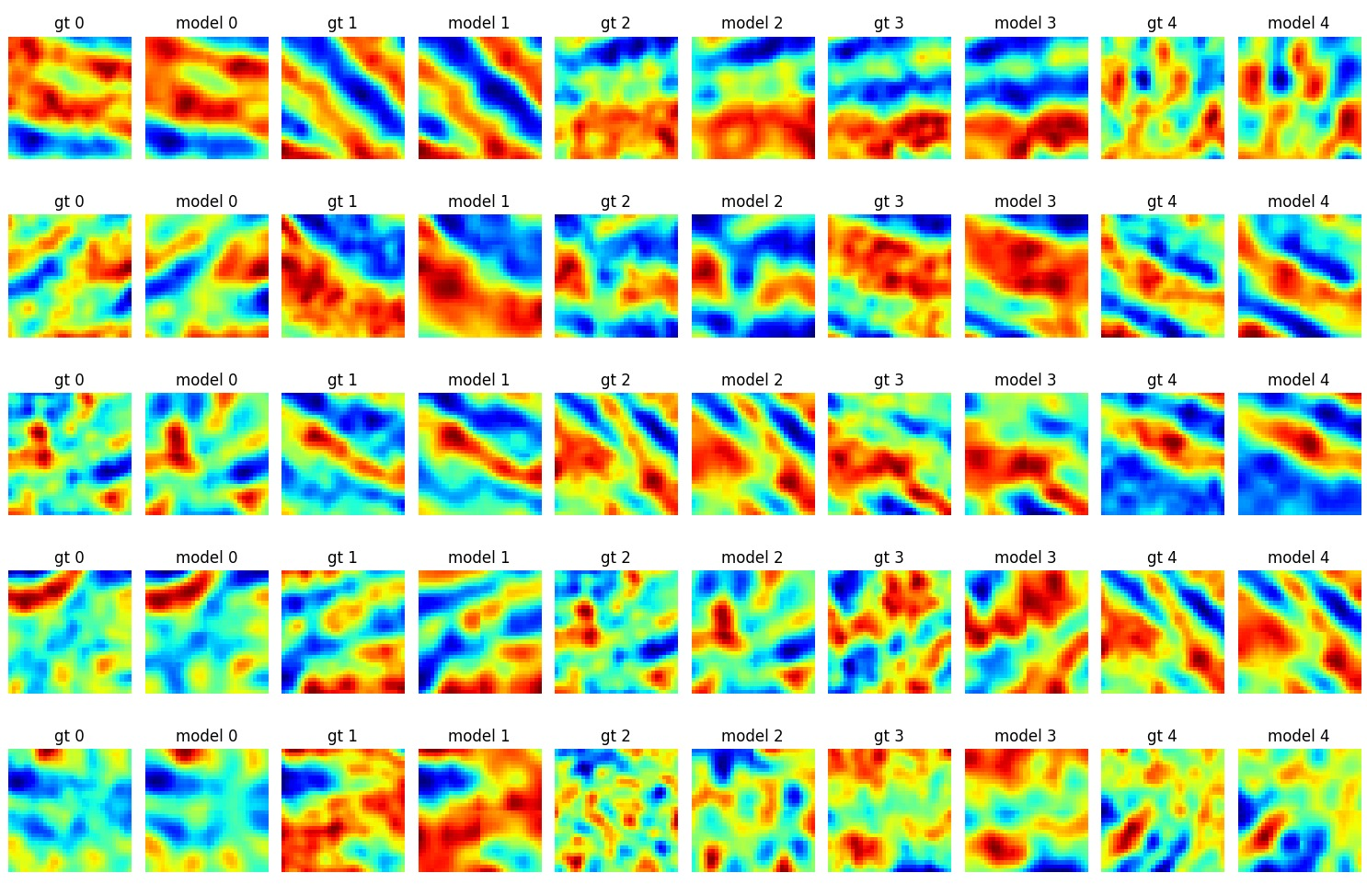which seems pretty reasonable to me, considering it was reconstructed from 512 parameters.
Estimating the ground truth:
This did not go very well. I adjusted the last output layer of the 3d convolutional kernel so that it output 2 channels rather than 3. The net then output this after a night of training:
… it appears that everything that is scroll is white and everything that is ground truth is black. The ol’ “here’s the mean of your dataset” trick. There’s no real proper reason why it is that I should be training on the reconstruction as well as the ground truth though, so if I just drop that hopefully that will make it better at training on the ground truth.
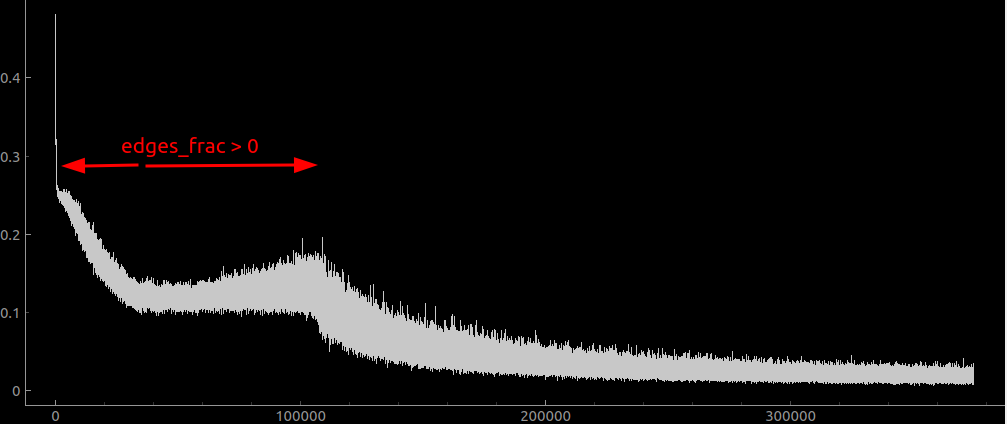
I have also added a bit of code that trains on patches that at the edge of ink and no ink, so it doesn’t bias too much towards ‘no ink’ since that’s most of the dataset:
def get_first_gt_x(out_vol: torch.tensor, out_gt: torch.tensor, path=GT1_PATH, edges=True):
gc.collect()
# out_vol is a N x 64 x 64 x 64 tensor, because the gt is 64 thick.
# out_gt is an N x 64 x 64 tensor from the gt image.
# n = out_vol.shape[0]
batch_sz, d_sz, w_sz, h_sz = out_vol.shape
start_y = 4600; start_x = 5800
end_y = 7000; end_x = 9300
assert(out_vol.shape[0] == out_gt.shape[0])
with Image.open(os.path.join(path, 'inklabels.png')) as img:
gt = np.array(img)
gt = torch.from_numpy(gt).to(torch.float32)
size = torch.tensor(gt.shape)
print(f"loaded gt of shape {gt.shape}")
x_out = torch.randint(start_x, end_x, (batch_sz,))
y_out = torch.randint(start_y, end_y, (batch_sz,))
if edges: # Only train on stuff with a bit of 0 and a bit of 1
torch.set_default_device('cuda')
no_edges = gt.clone()
# mask off the edge of the image so we don't index beyond it.
no_edges[0:w_sz // 2, :] = 0
no_edges[-w_sz // 2:, :] = 0
no_edges[:, 0:h_sz // 2] = 0
no_edges[:, -h_sz // 2:] = 0
edge_x = torch.diff(gt, dim=0, append=gt[-1, :].unsqueeze(0))
edge_y = torch.diff(gt, dim=1, append=gt[:, -1].unsqueeze(1))
edge = torch.logical_or(edge_x, edge_y)
edge_locs = torch.argwhere(edge).cuda()
n_edges = edge_locs.shape[0]
chosen_indices = torch.randint(0, n_edges, (batch_sz,))
chosen_corners = edge_locs[chosen_indices]
x_out = chosen_corners[:, 0] - w_sz // 2
y_out = chosen_corners[:, 1] - h_sz // 2
for b_idx in range(batch_sz):
out_gt[b_idx] = gt[x_out[b_idx]:x_out[b_idx]+w_sz, y_out[b_idx]:y_out[b_idx]+h_sz]
for z_idx in range(d_sz):
layer = load_tif_cached(os.path.join(path, f"surface_volume/{z_idx:02d}.tif"), size.tolist(), check=z_idx==0)
for b_idx in range(batch_sz):
out_vol[b_idx, z_idx] = layer[x_out[b_idx]:x_out[b_idx]+w_sz, y_out[b_idx]:y_out[b_idx]+h_sz]
print(f"loaded layer {z_idx}")Effects of residual layers:
The implementation of the residual layer courtesy of chatgpt as usual (it got the dims wrong though, also as usual):
class ResidualBlock3d(nn.Module):
def __init__(self, in_channels, out_channels, conv_layer):
super(ResidualBlock3d, self).__init__()
# Main path layers
self.conv1 = conv_layer(in_channels, out_channels, kernel_size=2, stride=2)
self.bn1 = nn.BatchNorm3d(out_channels)
self.conv2 = nn.Conv3d(out_channels, out_channels, kernel_size=3, stride=1, padding=1)
# Shortcut path layer - always using 1x1 convolution
if isinstance(conv_layer, nn.Conv3d):
self.shortcut = conv_layer(in_channels, out_channels, kernel_size=1, stride=2)
else:
self.shortcut = conv_layer(in_channels, out_channels, kernel_size=2, stride=2)
def forward(self, x):
residual = self.shortcut(x)
out = F.relu(self.bn1(self.conv1(x)))
out = self.conv2(out)
out += residual
out = F.relu(out)
return out
...
self.encs = nn.ModuleList()
self.encs.append(nn.Conv3d(1, expansion_init, kernel_size=2, stride=2))
for i in range(layers):
in_channels = expansion_init * 2**i
out_channels = expansion_init * 2**(i+1)
# self.encs.append(nn.Conv3d(in_channels, out_channels, kernel_size=2, stride=2))
self.encs.append(nn.Sequential(
nn.Conv3d(in_channels, out_channels, kernel_size=2, stride=2),
nn.Conv3d(out_channels, out_channels, kernel_size=3, stride=1, padding=1),
nn.BatchNorm3d(out_channels)
))
...
self.decs = nn.ModuleList()
for i in range(layers):
in_channels = final_expansion // 2**i
out_channels = final_expansion // 2**(i+1)
# either this:
self.decs.append(nn.Sequential(
nn.ConvTranspose3d(in_channels,out_channels, kernel_size=2, stride=2),
nn.Conv3d(out_channels, out_channels, kernel_size=3, stride=1, padding=1),
nn.BatchNorm3d(out_channels)
))
# or this
# self.decs.append(ResidualBlock3d(in_channels, out_channels, nn.ConvTranspose3d))
self.decs.append(nn.ConvTranspose3d(final_expansion // 2**layers, 1, kernel_size=2, stride=2))
Here is my net after training with 1000 iterations, no residual layers:
And here is 1000 iterations with residual layers:
“
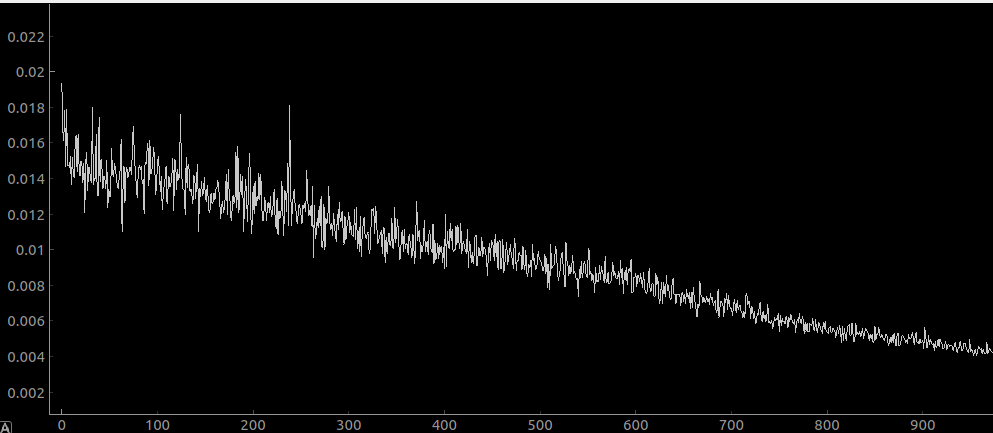
Yuuuuuge difference!! The net with no residuals looks like it has flatlined, but it actually hasn’t. It seems to train about 10x slower is all.
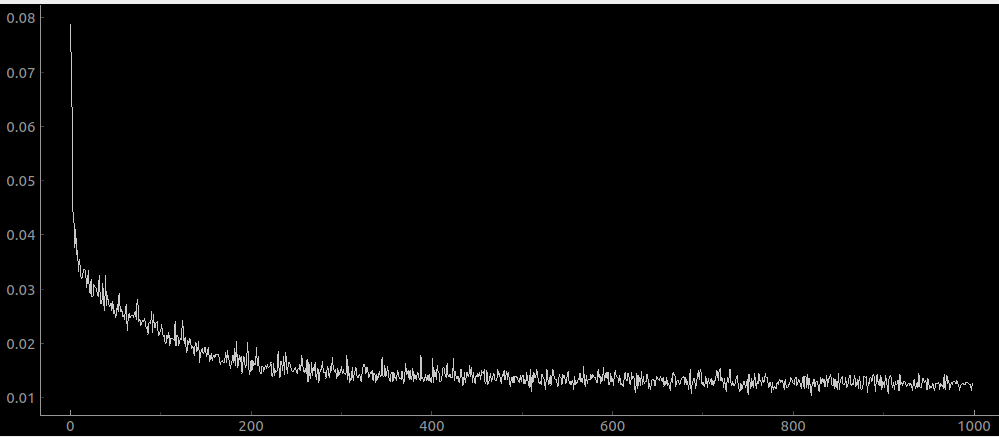
Overfitting
I was training the net on 1000 examples, then reloading a new set of 1000 examples from the scroll every 1000 iterations. That leads to a loss curve that looks like this:
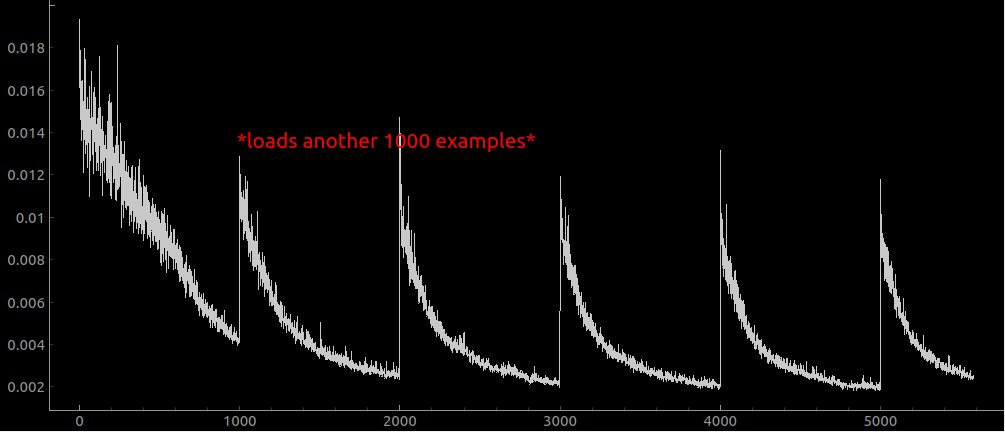
When I change this to 10000 examples, I get a loss curve that looks like this:
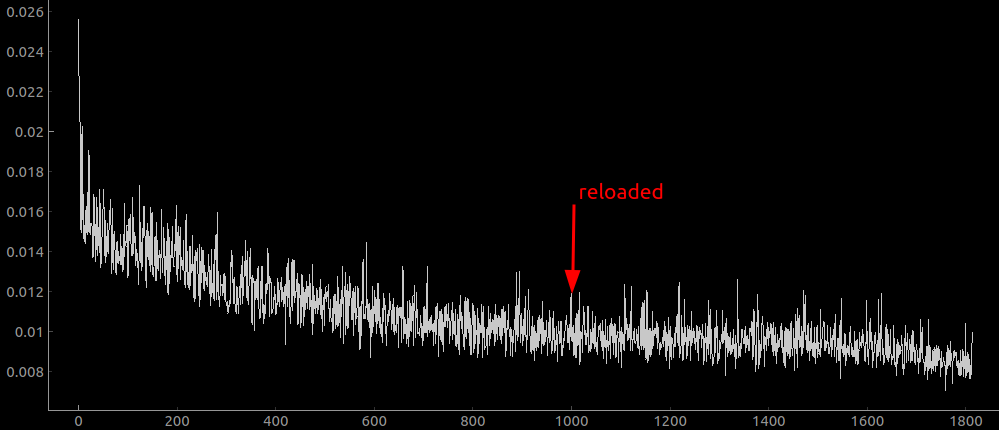
so you can see that there is no overfitting already, but also the net has like 10x higher loss! it’s about as high as when there were no residual layers! is this a coincidence? Here is the net trained on a dataset size of 1e4, with no residual layers:
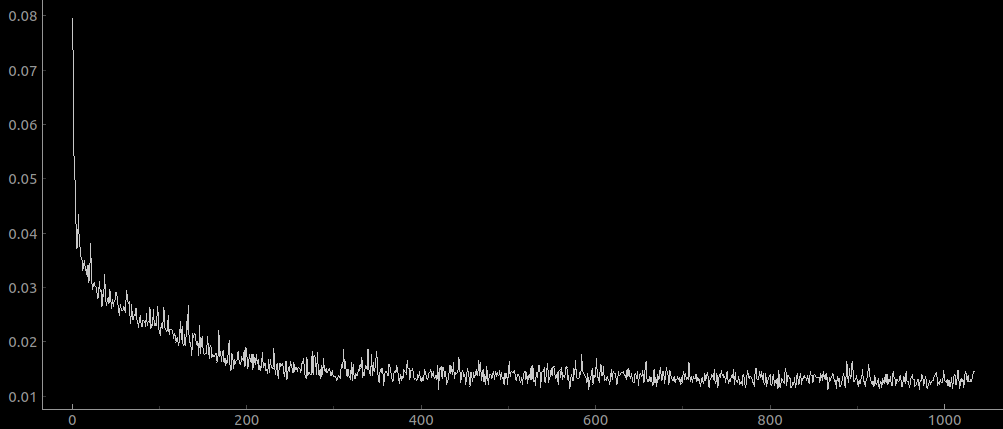
…about the same as with a dataset size of 1e3 from before. This makes me update rather strongly towards “residual connections are great for overfitting” and away from “residual connections are good for avoiding exploding gradients”.
Training on ink: initial results
Here is the result of simply switching the target volume from reconstructing the original to reconstructing the ground truth:
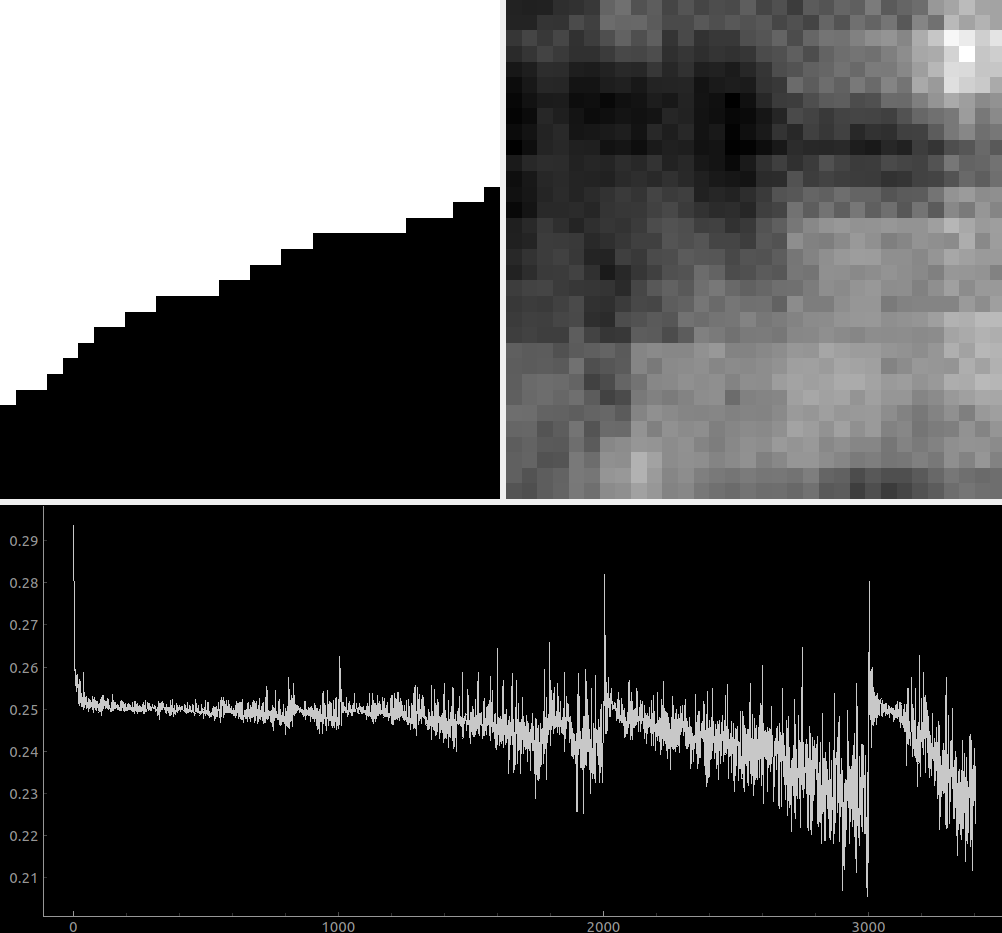
Looks like it’s doing a reasonable job of remembering the dataset just like before, although remembering the ink seems to be harder. Still though, it shows there is some correlation between what is desired on the input and what is desired on the output so that’s nice.
When I leave this to train for an hour or so on parts of the dataset that contain only an edge it actually does quite well. But when I plot the results of this:
…yeah, if all it sees is an edge, all it’s gonna output is an edge.
One other thing I’m running into here is loading times - significant parts of the training time are spent loading data. So speeding that up is a good next step I think.
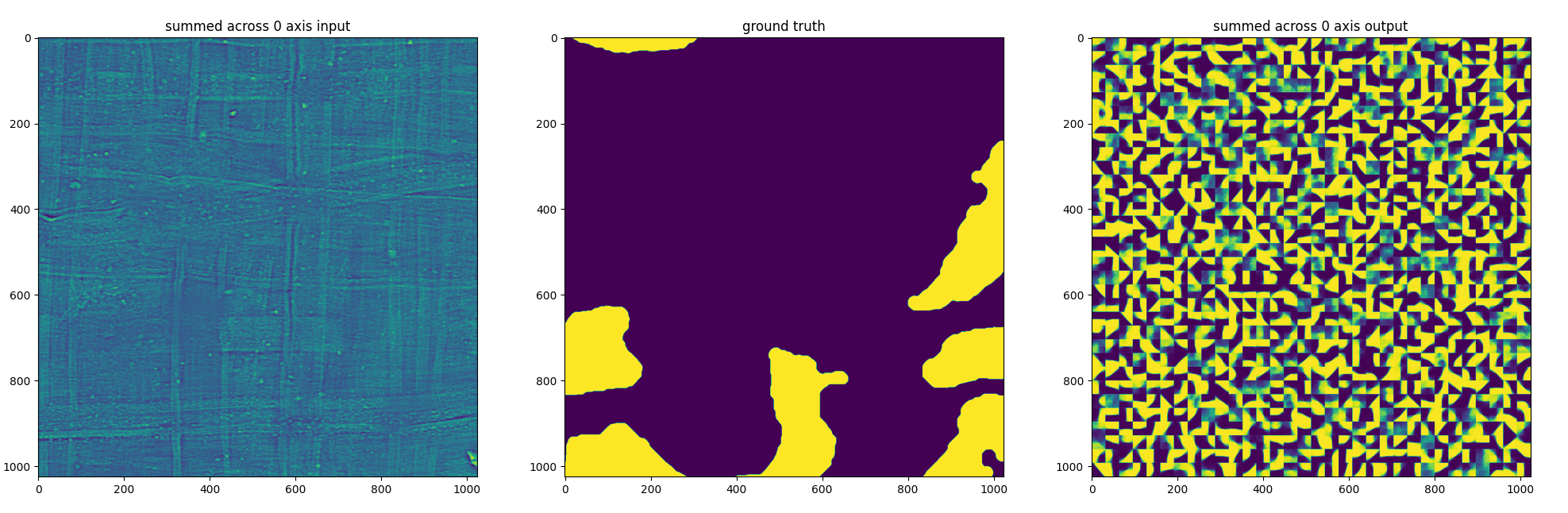
Attempt at a proper run
I got rid of the code for training on only data around edges - I put that in because of the garbage that I got out before. Here is the loss curve for a true sampling of the input, attempting to reconstruct the output:
This too is exhibiting weird behaviors: big spikes, and this super long period of plateauing prior to the net ‘picking up’ the gradient again.
Results after a few hours training
I did this over a couple of different restarts so I don’t have a good screenshot of the loss over time, but here is the final result:
…Looks pretty good to me!
Here is what it looks like zoomed in on some random blob:
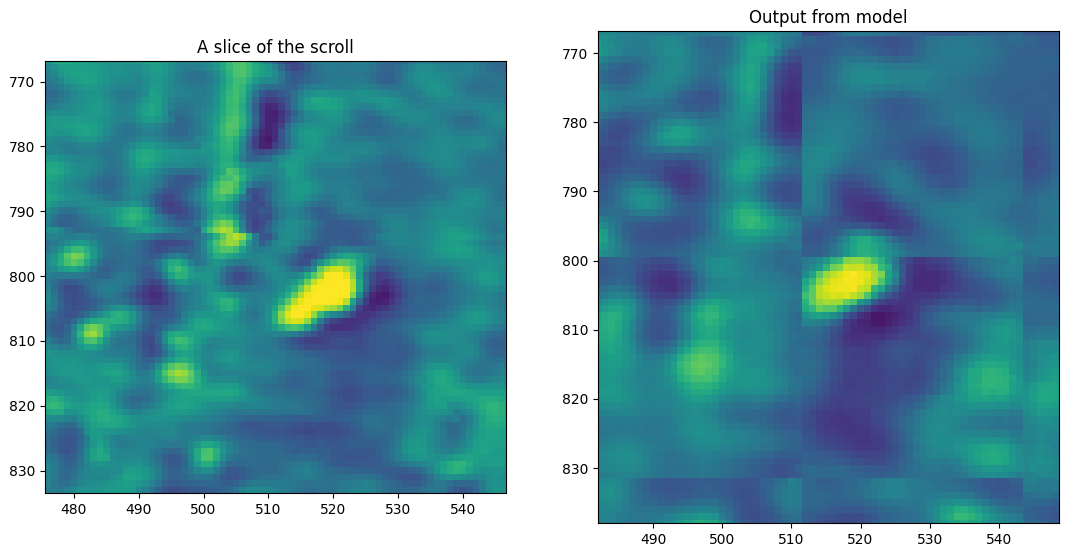
…so you can see that the boundaries of the model are clearly visible. Presumably this would be improve if a bunch of model outputs were averaged with different offsets. It might also be good to examine the loss as a function of the distance from the center of the cube - if there are edge effects it might be a good idea to discard them.
Attempt at training on ground truth overnight:
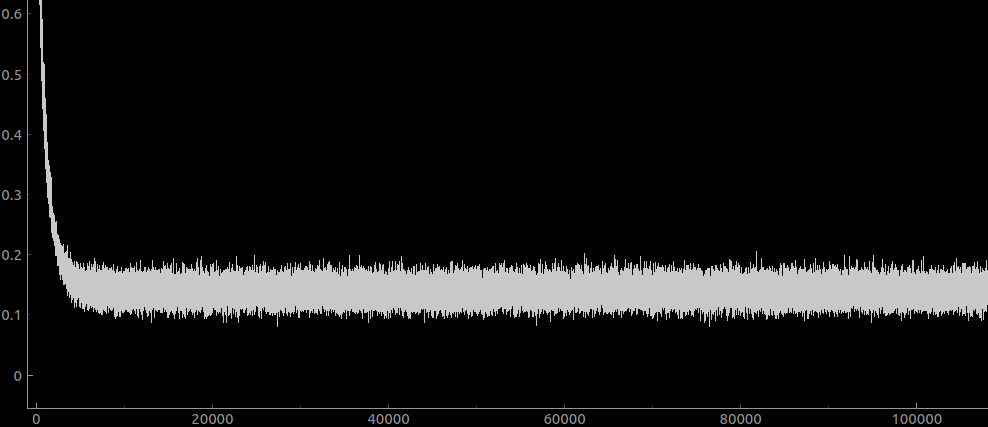Looks like it plaeaued super quick there. This started with a learning rate of 3e-5 and went to 3e-7. it used the background thread data loading technique.
And here is what that same model looks like trying to guess where the ink is:
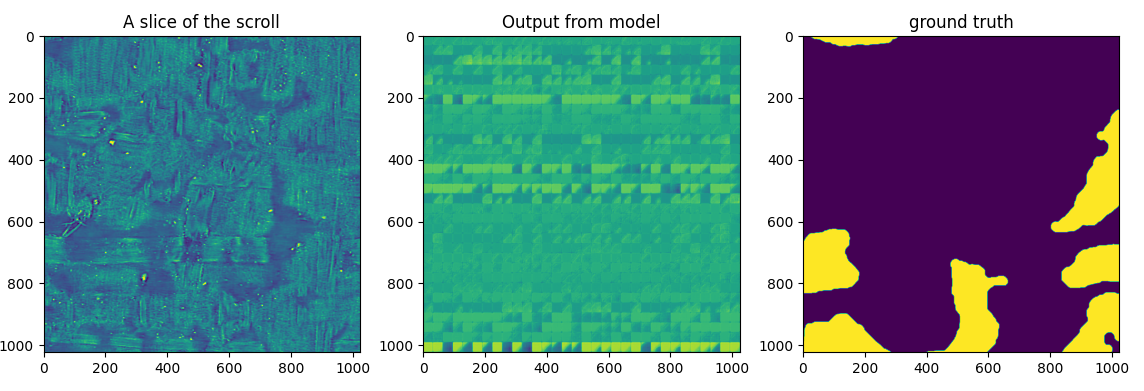
oh well.
???
Having all these weird failures to train made me try to go back and replicate my previous successfull results. Here are the results of training overnight a 32 cube reconstruction:
Pretty garbage. I wonder if this is because I had a learning rate schedule that started at 3e-4 and went down to 3e-6. So I will load this model where it stopped and try again with a constant rate of 3e-4.
And here is <1 hour of training with a learning rate of 3e-4:
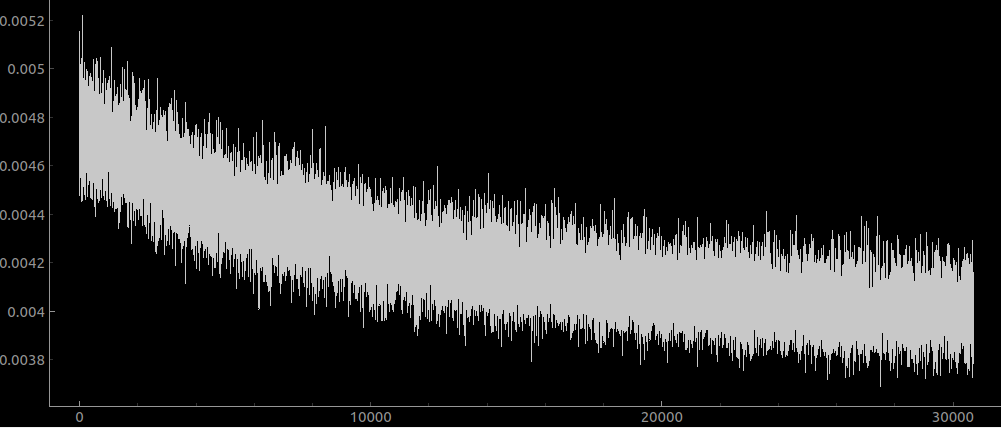
So I think that this means that the learning rate towards the end was indeed too small.
Batch size
I have been training with a batch size of 256, which is well below the max that will fit in my GPU. There are two reasons to increase batch size:
- Better utilisation of The GPU since the weights loaded from memory can be used many times
- Better estimation of the gradient
The last one mostly seems bogus to me tbh, so I have not been putting effort into filling up the GPU. My intuition here was basically that the estimation of the gradient would go with sqrt (batch size), so instead of having a batch size of (say) 4, you should have a batch size of 1 and increment a small amount 4 times. IRL you still want a batch size >> 1 because of point 1 about GPU utilisation and so what I have been doing is increasing the batch size until
nvidia-smisaid that I was using as much power as I could.
As a small and highly invalid experiment, here is me setting a breakpoint during training and setting the batch size from 256→1024.
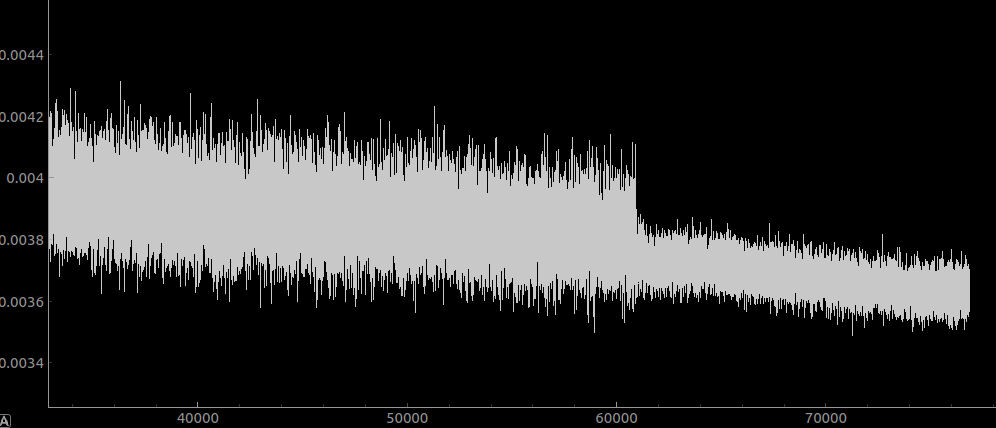
…it doesn’t look like it is having much effect here. Remember in the same time that I do 1 batch-size-1024 iteration I can do 4 of the 256 variant. I’ll keep the experiment running for a bit more just to see what happens though. Given that there was no change in the learning rate from 256→1024 batch size, this clearly means we need to go lower!
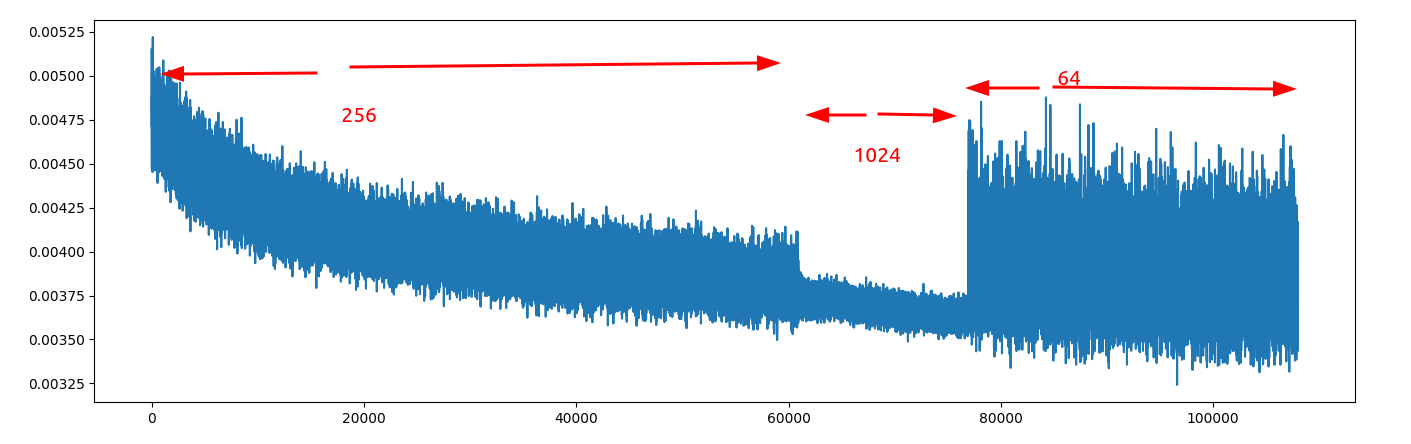
Above I ran with three different batch sizes. It kind of looks like the mean loss changed with the batch size (I don’t know how that could be) but the learning rate didn’t really.
Experiment: learning rate
Here is a learning rate of 3e-4 overnight:
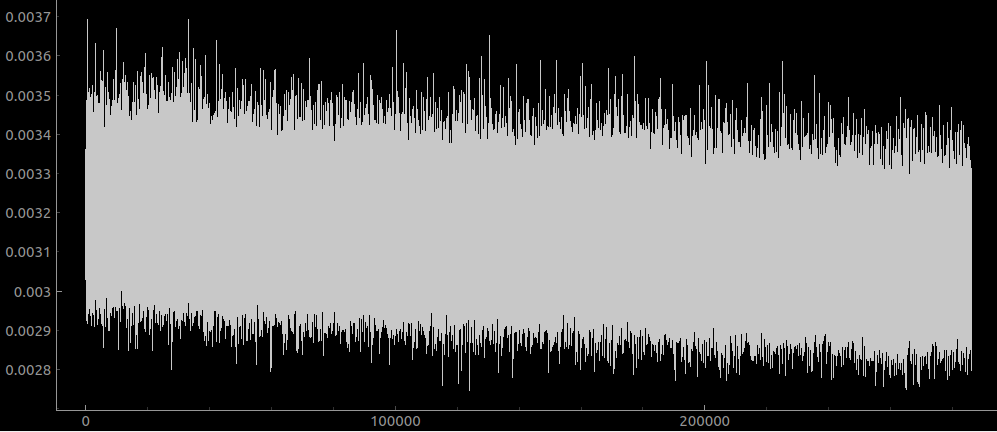Looks it like it just keeps learning! I was actually busy for a few days after this so let it run even longer, and the loss just kept on dropping. From the y axis you can see that the absolute level of improvement is not that great though.
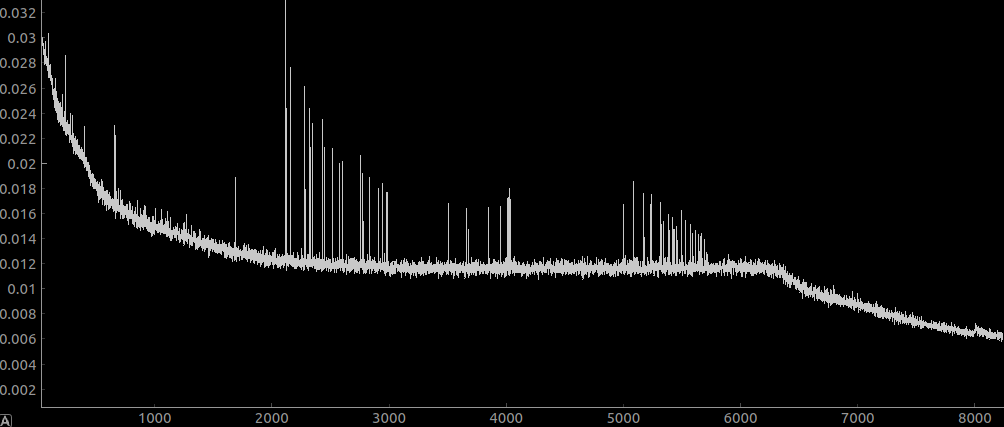
Distribution
I haven’t been normalising the input to my net. It occurs to me that this is a bad idea. here is a histogram of the density across the whole ground truth scroll (after converting from uint16 to float):
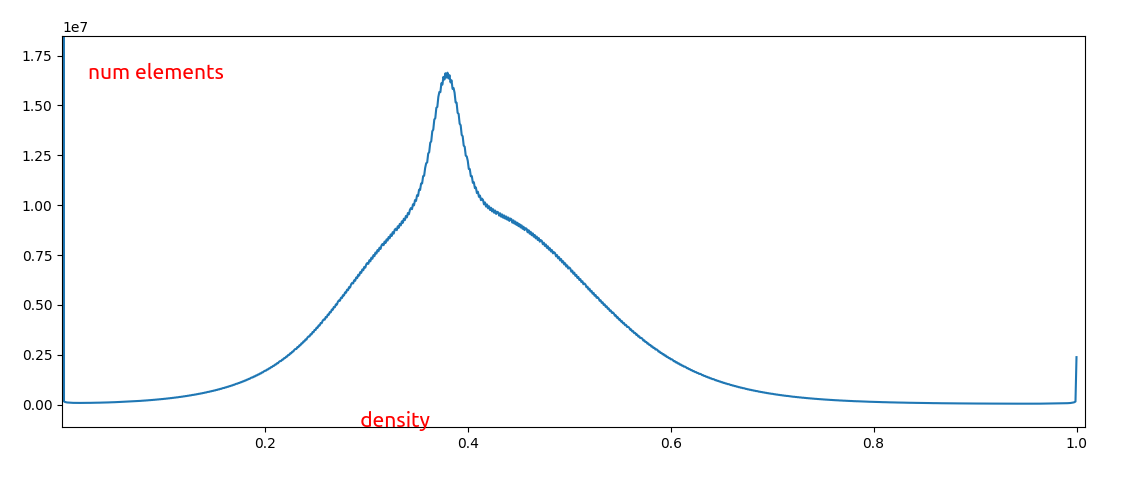honestly I think my instincts are right here and this is a pretty boring distribution that doesn’t need anything done to it for a net to be able to understand it.
exp about classifying on frozen layers.
